2016-2017学年天津市南开区九年级上学期期中数学试卷
试卷更新日期:2016-12-21 类型:期中考试
一、选择题
-
1. 一元二次方程x(x+5)=0的根是( )A、x1=0,x2=5 B、x1=0,x2=﹣5 C、x1=0,x2= D、x1=0,x2=﹣2. 下列四个图形中属于中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 已知二次函数y=3x2+c与正比例函数y=4x的图象只有一个交点,则c的值为( )A、 B、 C、3 D、44. 抛物线y=﹣3x2+12x﹣7的顶点坐标为( )A、(2,5) B、(2,﹣19) C、(﹣2,5) D、(﹣2,﹣43)5. 由二次函数y=2(x﹣3)2+1可知( )A、其图象的开口向下 B、其图象的对称轴为x=﹣3 C、其最大值为1 D、当x<3时,y随x的增大而减小6. 如图中∠BOD的度数是( )
3. 已知二次函数y=3x2+c与正比例函数y=4x的图象只有一个交点,则c的值为( )A、 B、 C、3 D、44. 抛物线y=﹣3x2+12x﹣7的顶点坐标为( )A、(2,5) B、(2,﹣19) C、(﹣2,5) D、(﹣2,﹣43)5. 由二次函数y=2(x﹣3)2+1可知( )A、其图象的开口向下 B、其图象的对称轴为x=﹣3 C、其最大值为1 D、当x<3时,y随x的增大而减小6. 如图中∠BOD的度数是( ) A、150° B、125° C、110° D、55°7. 如图,点E在y轴上,⊙E与x轴交于点A,B,与y轴交于点C,D,若C(0,9),D(0,﹣1),则线段AB的长度为( )
A、150° B、125° C、110° D、55°7. 如图,点E在y轴上,⊙E与x轴交于点A,B,与y轴交于点C,D,若C(0,9),D(0,﹣1),则线段AB的长度为( ) A、3 B、4 C、6 D、88. 如图,AB是圆O的直径,C,D是圆O上的点,且OC∥BD,AD分别与BC,OC相交于点E,F.则下列结论:
A、3 B、4 C、6 D、88. 如图,AB是圆O的直径,C,D是圆O上的点,且OC∥BD,AD分别与BC,OC相交于点E,F.则下列结论:①AD⊥BD;②∠AOC=∠ABC;③CB平分∠ABD;④AF=DF;⑤BD=2OF.
其中一定成立的是( )
 A、①③⑤ B、②③④ C、②④⑤ D、①③④⑤9. 《九章算术》是我国古代内容极为丰富的数学名著,书中有下列问题“今有勾八步,股十五步,问勾中容圆径几何?”其意思是:“今有直角三角形,勾(短直角边)长为8步,股(长直角边)长为15步,问该直角三角形能容纳的圆形(内切圆)直径是多少?”( )
A、①③⑤ B、②③④ C、②④⑤ D、①③④⑤9. 《九章算术》是我国古代内容极为丰富的数学名著,书中有下列问题“今有勾八步,股十五步,问勾中容圆径几何?”其意思是:“今有直角三角形,勾(短直角边)长为8步,股(长直角边)长为15步,问该直角三角形能容纳的圆形(内切圆)直径是多少?”( ) A、3步 B、5步 C、6步 D、8步10. 如图,在△ABC中,∠CAB=65°,将△ABC在平面内绕点A旋转到△AB′C′的位置,使CC′∥AB,则旋转角的度数为( )
A、3步 B、5步 C、6步 D、8步10. 如图,在△ABC中,∠CAB=65°,将△ABC在平面内绕点A旋转到△AB′C′的位置,使CC′∥AB,则旋转角的度数为( ) A、35° B、40° C、50° D、65°11. 以半径为2的圆的内接正三角形、正方形、正六边形的边心距为三边作三角形,则该三角形的面积是( )A、 B、 C、 D、12. 如图,正方形ABCD中,AB=8cm,对角线AC,BD相交于点O,点E,F分别从B,C两点同时出发,以1cm/s的速度沿BC,CD运动,到点C,D时停止运动,设运动时间为t(s),△OEF的面积为s(cm2),则s(cm2)与t(s)的函数关系可用图象表示为( )
A、35° B、40° C、50° D、65°11. 以半径为2的圆的内接正三角形、正方形、正六边形的边心距为三边作三角形,则该三角形的面积是( )A、 B、 C、 D、12. 如图,正方形ABCD中,AB=8cm,对角线AC,BD相交于点O,点E,F分别从B,C两点同时出发,以1cm/s的速度沿BC,CD运动,到点C,D时停止运动,设运动时间为t(s),△OEF的面积为s(cm2),则s(cm2)与t(s)的函数关系可用图象表示为( )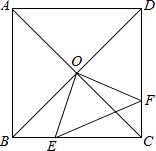 A、
A、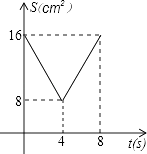 B、
B、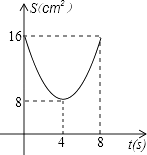 C、
C、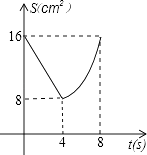 D、
D、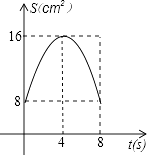
二、填空题
-
13. 点P(2,﹣1)关于原点的对称点坐标为P′(m,1),则m= .14. 如图,在平面直角坐标系xOy中,已知点A(3,4),将OA绕坐标原点O逆时针旋转90°至OA′,则点A′的坐标是 .
 15. 关于x的二次函数y=x2﹣kx+k﹣2的图象与y轴的交点在x轴的上方,请写出一个满足条件的二次函数的表达式: .16. 如图,抛物线y=ax2+bx+c与x轴的一个交点是A(1,0),对称轴为直线x=﹣1,则一元二次方程ax2+bx+c=0的解是 .
15. 关于x的二次函数y=x2﹣kx+k﹣2的图象与y轴的交点在x轴的上方,请写出一个满足条件的二次函数的表达式: .16. 如图,抛物线y=ax2+bx+c与x轴的一个交点是A(1,0),对称轴为直线x=﹣1,则一元二次方程ax2+bx+c=0的解是 . 17. 某种植物的主干长出若干数目的支干又长出同样数目的小分支,主干、支干和小分支的总数是91.设每个支干长出x个小分支,则可得方程为 .18. 如图,AB是⊙O的一条弦,C是⊙O上一动点且∠ACB=45°,E,F分别是AC,BC的中点,直线EF与⊙O交于点G,H.若⊙O的半径为2,则GE+FH的最大值为 .
17. 某种植物的主干长出若干数目的支干又长出同样数目的小分支,主干、支干和小分支的总数是91.设每个支干长出x个小分支,则可得方程为 .18. 如图,AB是⊙O的一条弦,C是⊙O上一动点且∠ACB=45°,E,F分别是AC,BC的中点,直线EF与⊙O交于点G,H.若⊙O的半径为2,则GE+FH的最大值为 .
三、解答题
-
19. 按要求解一元二次方程:(1)、x(x+4)=8x+12(适当方法)(2)、3x2﹣6x+2=0(配方法)20. 在直角坐标平面内,二次函数图象的顶点为A(1,﹣4),且过点B(3,0).
 (1)、求该二次函数的解析式;(2)、将该二次函数图象向右平移几个单位,可使平移后所得图象经过坐标原点?并直接写出平移后所得图象与x轴的另一个交点的坐标.21. 如图,AB是圆O的直径,CD是圆O的一条弦,且CD⊥AB于点E.
(1)、求该二次函数的解析式;(2)、将该二次函数图象向右平移几个单位,可使平移后所得图象经过坐标原点?并直接写出平移后所得图象与x轴的另一个交点的坐标.21. 如图,AB是圆O的直径,CD是圆O的一条弦,且CD⊥AB于点E. (1)、若∠A=48°,求∠OCE的度数;(2)、若CD=4 ,AE=2,求圆O的半径.22. 如图,△ABC 中,AB=AC,以AB为直径作⊙O,与BC交于点D,过D作AC的垂线,垂足为E.证明:
(1)、若∠A=48°,求∠OCE的度数;(2)、若CD=4 ,AE=2,求圆O的半径.22. 如图,△ABC 中,AB=AC,以AB为直径作⊙O,与BC交于点D,过D作AC的垂线,垂足为E.证明: (1)、BD=DC;(2)、DE是⊙O切线.23. 如图,要建一个长方形养鸡场,鸡场的一边靠墙(墙足够长),如果用50m长的篱笆围成中间有一道篱笆墙的养鸡场,设它的长度为x(篱笆墙的厚度忽略不计).
(1)、BD=DC;(2)、DE是⊙O切线.23. 如图,要建一个长方形养鸡场,鸡场的一边靠墙(墙足够长),如果用50m长的篱笆围成中间有一道篱笆墙的养鸡场,设它的长度为x(篱笆墙的厚度忽略不计). (1)、要使鸡场面积最大,鸡场的长度应为多少米?(2)、如果中间有n(n是大于1的整数)道篱笆墙,要使鸡场面积最大,鸡场的长应为多少米?比较(1)(2)的结果,要使鸡场面积最大,鸡场长度与中间隔离墙的道数有怎样的关系?24. 如图,点C为线段AB上一点,△ACM,△CBN是等边三角形,直线AN,MC交于点E,直线BM,CN交于点F.
(1)、要使鸡场面积最大,鸡场的长度应为多少米?(2)、如果中间有n(n是大于1的整数)道篱笆墙,要使鸡场面积最大,鸡场的长应为多少米?比较(1)(2)的结果,要使鸡场面积最大,鸡场长度与中间隔离墙的道数有怎样的关系?24. 如图,点C为线段AB上一点,△ACM,△CBN是等边三角形,直线AN,MC交于点E,直线BM,CN交于点F.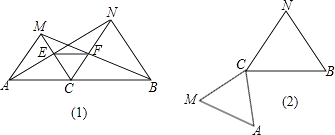 (1)、求证:AN=MB;(2)、求证:△CEF为等边三角形;(3)、将△ACM绕点C按逆时针方向旋转90°,其他条件不变,在(2)中画出符合要求的图形,并判断(1)(2)题中的两结论是否依然成立.并说明理由.25. 如图,在平面直角坐标系中,圆M经过原点O,且与x轴、y轴分别相交于A(﹣8,0),B(0,﹣6)两点.
(1)、求证:AN=MB;(2)、求证:△CEF为等边三角形;(3)、将△ACM绕点C按逆时针方向旋转90°,其他条件不变,在(2)中画出符合要求的图形,并判断(1)(2)题中的两结论是否依然成立.并说明理由.25. 如图,在平面直角坐标系中,圆M经过原点O,且与x轴、y轴分别相交于A(﹣8,0),B(0,﹣6)两点. (1)、求出直线AB的函数解析式;(2)、若有一抛物线的对称轴平行于y轴且经过点M,顶点C在圆M上,开口向下,且经过点B,求此抛物线的函数解析式;(3)、设(2)中的抛物线交x轴于D、E两点,在抛物线上是否存在点P,使得S△PDE= S△ABC?若存在,请求出点P的坐标;若不存在,请说明理由.
(1)、求出直线AB的函数解析式;(2)、若有一抛物线的对称轴平行于y轴且经过点M,顶点C在圆M上,开口向下,且经过点B,求此抛物线的函数解析式;(3)、设(2)中的抛物线交x轴于D、E两点,在抛物线上是否存在点P,使得S△PDE= S△ABC?若存在,请求出点P的坐标;若不存在,请说明理由.