2016-2017学年山东省济宁市兖州区九年级上学期期中数学试卷
试卷更新日期：2016-12-21 类型：期中考试
一、选择题
-
1. 下列汽车标志中既是轴对称图形又是中心对称图形的是（ ）A、
B、
C、
D、
2. 如图，在半径为5的⊙O中，弦AB=6，OP⊥AB，垂足为点P，则OP的长为（ ）
A、3 B、2.5 C、4 D、3.53. 如图，在⊙O中， = ，∠AOB=40°，则∠ADC的度数是（ ）
A、40° B、30° C、20° D、15°4. 用配方法解一元二次方程x2+4x﹣3=0时，原方程可变形为（ ）A、（x+2）2=1 B、（x+2）2=7 C、（x+2）2=13 D、（x+2）2=195. 方程2x2=3x的解为（ ）A、0 B、 C、- D、0，6. 如图所示，将一个含30°角的直角三角板ABC绕点A旋转，使得点B，A，C′在同一条直线上，则三角板ABC旋转的角度是（ ）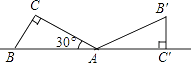
A、60° B、90° C、120° D、150°7. 有x支球队参加篮球比赛，共比赛了45场，每两队之间都比赛一场，则下列方程中符合题意的是（ ）A、 x（x﹣1）=45 B、 x（x+1）=45 C、x（x﹣1）=45 D、x（x+1）=458. 如图，假设篱笆（虚线部分）的长度16m，则所围成矩形ABCD的最大面积是（ ）
A、60m2 B、63m2 C、64m2 D、66m29. 二次函数y=ax2+bx+c（a≠0）图象上部分点的坐标（x，y）对应值列表如下：x
…
﹣3
﹣2
﹣1
0
1
…
y
…
﹣3
﹣2
﹣3
﹣6
﹣11
…
则该函数图象的对称轴是（ ）
A、直线x=﹣3 B、直线x=﹣2 C、直线x=﹣1 D、直线x=010.二次函数y=ax2+bx+c（a≠0）的图象如图所示，下列结论：①b＜0；②c＞0；③a+c＜b；④b2﹣4ac＞0，其中正确的个数是（ ）
A、1 B、2 C、3 D、4二、填空题
-
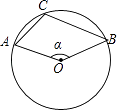
11. 已知关于x的方程x2+x+2a﹣1=0的一个根是0，则a= ．12. 方程（x﹣1）2=4的根是 ．13. 若二次函数y=x2+2x+m的图象与x轴没有公共点，则m的取值范围是 ．14. 如图，在⊙O中，点A，B，C在⊙O上，且∠ACB=110°，则∠α= ．
15. 如图，在平面直角坐标系中，菱形OABC的顶点A在x轴正半轴上，顶点C的坐标为（4，3），D是抛物线y=﹣x2+6x上一点，且在x轴上方，则△BCD面积的最大值为 ．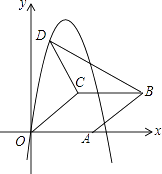
三、解答题
-
16. 关于x的一元二次方程x2+（2m+1）x+m2﹣1=0有两个不相等的实数根．(1)、求m的取值范围；(2)、写出一个满足条件的m的值，并求此时方程的根．17. 如图，在平面直角坐标系中，已知△ABC的三个顶点的坐标分别为A（﹣3，5），B（﹣2，1），C（﹣1，3）．
①若△ABC经过平移后得到△A1B1C1 ， 已知点C1的坐标为（4，0），写出顶点A1 ， B1的坐标；
②若△ABC和△A2B2C2关于原点O成中心对称图形，写出△A2B2C2的各顶点的坐标；
③将△ABC绕着点O按顺时针方向旋转90°得到△A3B3C3 ， 写出△A3B3C3的各顶点的坐标．
18. 为进一步发展基础教育，自2014年以来，某县加大了教育经费的投入，2014年该县投入教育经费6000万元.2016年投入教育经费8640万元．假设该县这两年投入教育经费的年平均增长率相同．(1)、求这两年该县投入教育经费的年平均增长率；(2)、若该县教育经费的投入还将保持相同的年平均增长率，请你预算2017年该县投入教育经费多少万元．19. 如图，已知抛物线y=﹣x2+mx+3与x轴交于A，B两点，与y轴交于点C，点B的坐标为（3，0）
(1)、求m的值及抛物线的顶点坐标．(2)、点P是抛物线对称轴l上的一个动点，当PA+PC的值最小时，求点P的坐标．20. 某商店原来平均每天可销售某种水果200千克，每千克可盈利6元，为减少库存，经市场调查，如果这种水果每千克降价1元，则每天可所多售出20千克．(1)、设每千克水果降价x元，平均每天盈利y元，试写出y关于x的函数表达式；(2)、若要平均每天盈利960元，则每千克应降价多少元？
