2016-2017学年北京五十六中九年级上学期期中数学试卷

试卷更新日期：2016-12-21 类型：期中考试

进入出卷网下载

一、选择题

1. 抛物线y=2（x﹣3）²+1的顶点坐标是（）

A、（3，1） B、（3，﹣1） C、（﹣3，1） D、（﹣3，﹣1）

查看试题解析
2. 抛物线y=（x+2）²﹣3的对称轴是（）

A、直线x=﹣3 B、直线x=3 C、直线x=2 D、直线x=﹣2

查看试题解析
3.
如图，⊙O是△ABC的外接圆，若∠ABC=40°，则∠AOC的度数为（　　）

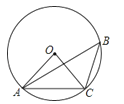A、20° B、40° C、60° D、80°

查看试题解析
4. 将二次函数y=x²﹣6x+5用配方法化成y=（x﹣h）²+k的形式，下列结果中正确的是（　　）

A、y=（x﹣6）²+5 B、y=（x﹣3）²+5 C、y=（x﹣3）²﹣4 D、y=（x+3）²﹣9

查看试题解析
5. 将抛物线y=3x²+1的图像向左平移2个单位，再向下平移3个单位，得到的抛物线是（）

A、y=3（x+2）²﹣3 B、y=3（x+2）²﹣2 C、y=3（x﹣2）²﹣3 D、y=3（x﹣2）²﹣2

查看试题解析
6. 二次函数y=kx²﹣6x+3的图象与x轴有交点，则k的取值范围是（　　）

A、k＜3 B、k＜3且k≠0 C、k≤3 D、k≤3且k≠0

查看试题解析
7. 如图，⊙C与∠AOB的两边分别相切，其中OA边与⊙C相切于点P．若∠AOB=90°，OP=6，则OC的长为（）

A、12 B、 $12 \sqrt{2}$ C、 $6 \sqrt{2}$ D、 $6 \sqrt{3}$

查看试题解析
8. 如图，A，B，C三点在已知的圆上，在△ABC中，∠ABC=70°，∠ACB=30°，D是 $\hat{B A C}$ 的中点，连接DB，DC，则∠DBC的度数为（）

A、30° B、45° C、50° D、70°

查看试题解析
9.
如图为二次函数y=ax²+bx+c的图象，下列各式中：①a＞0，②b＞0，③c=0，④c=1，⑤a+b+c=0．正确的只有（）

A、①④ B、②③④ C、③④⑤ D、①③⑤

查看试题解析

二、填空题

10. 若y=x^m^﹣²是二次函数，则m= ．

查看试题解析
11. 点A（﹣3，y₁），B（2，y₂）在抛物线y=x²﹣5x上，则y₁ y₂ ．（填“＞”，“＜”或“=”）

查看试题解析
12. 若二次函数y=x²+2m﹣1的图像经过原点，则m的值是．

查看试题解析
13. 如图，在平面直角坐标系xOy中，已知点A（3，4），将OA绕坐标原点O逆时针旋转90°至OA′，则点A′的坐标是．

查看试题解析
14.
程大位所著《算法统宗》是一部中国传统数学重要的著作．在《算法统宗》中记载：“平地秋千未起，踏板离地一尺．送行二步与人齐，五尺人高曾记．仕女佳人争蹴，终朝笑语欢嬉．良工高士素好奇，算出索长有几？”【注释】1步=5尺．
译文：“当秋千静止时，秋千上的踏板离地有1尺高，如将秋千的踏板往前推动两步（10尺）时，踏板就和人一样高，已知这个人身高是5尺．美丽的姑娘和才子们，每天都来争荡秋千，欢声笑语终日不断．好奇的能工巧匠，能算出这秋千的绳索长是多少吗？”
如图，假设秋千的绳索长始终保持直线状态，OA是秋千的静止状态，A是踏板，CD是地面，点B是推动两步后踏板的位置，弧AB是踏板移动的轨迹．已知AC=1尺，CD=EB=10尺，人的身高BD=5尺．设绳索长OA=OB=x尺，则可列方程为．

查看试题解析
15. 阅读下面材料：
在学习《圆》这一章时，老师给同学们布置了一道尺规作图题：
小敏的作法如下：
老师认为小敏的作法正确．
请回答：连接OA，OB后，可证∠OAP=∠OBP=90°，其依据是；由此可证明直线PA，PB都是⊙O的切线，其依据是．

查看试题解析

三、解答题

16. 解方程：x²﹣6x+5=0．

查看试题解析
17. 若二次函数的图象过（﹣3，0）、（1，0）、（0，﹣3）三点，求这个二次函数的解析式．

查看试题解析
18. 若二次函数y=ax²+bx+c的图像最高点为（1，3）经过（﹣1，0）两点，求此二次函数的解析式．

查看试题解析
19. 已知二次函数的解析式是y=x²﹣2x﹣3

(1)、用配方法将y=x²﹣2x﹣3化成y=a（x﹣h）²+k的形式；

(2)、在直角坐标系中，用五点法画出它的图像；

(3)、利用图象求当x为何值时，函数值y＜0

(4)、当x为何值时，y随x的增大而减小？

(5)、当﹣3＜x＜3时，观察图象直接写出函数值y的取值的范围．

查看试题解析
20. 如图所示，在⊙O中，CD是直径，AB是弦，AB⊥CD于M，CD=10cm，OM：OC=3：5，求弦AB的长．

查看试题解析
21. 如图，在平面直角坐标系中，四边形OABC四个顶点的坐标分别为O（0，0），A（﹣3，0），B（﹣4，2），C（﹣1，2）．将四边形OABC绕点O顺时针旋转90°后，点A，B，C分别落在点A′，B′，C′处．

(1)、请你在所给的直角坐标系中画出旋转后的四边形OA′B′C′；

(2)、点C旋转到点C′所经过的弧的半径是，点C经过的路线长是．

查看试题解析
22. 如图所示，已知AB是圆O的直径，圆O过BC的中点D，且DE⊥AC．

(1)、求证：DE是圆O的切线；

(2)、若∠C=30°，CD=10cm，求圆O的半径．

查看试题解析
23. 如图，二次函数y₁=ax²+bx+3的图像与x轴相交于点A（﹣3，0）、B（1，0），交y轴于点C，C，D是二次函数图象上的一对对称点，一次函数y₂=mx+n的图像经过B、D两点．

(1)、求二次函数的解析式及点D的坐标；

(2)、根据图像写出y₂＞y₁时，x的取值范围．

查看试题解析
24. 抛物线y=﹣x²+（m﹣1）x+m．

(1)、求证：无论m为何值，这条抛物线都与x轴至少有一个交点；

(2)、求它与x轴交点坐标A，B和与y轴的交点C的坐标；（用含m的代数式表示点坐标）

(3)、S_△_ABC=3，求抛物线的解析式．

查看试题解析
25. 某商人如果将进货价为8元的商品按每件10元出售，每天可销售100件，现采用提高售出价，减少进货量的办法增加利润，已知这种商品每涨价1元其销售量就要减少10件，

(1)、求该商品平均每天的利润y（元）与涨价x（元）之间的函数关系式；

(2)、问他将售出价定为多少元时，才能使每天所赚的利润最大？并求出最大利润；

(3)、若每件商品的售价不高于13元，那么将售价定为多少元时，可以获最大利润？

查看试题解析
26.
阅读下面材料：
如图1，在平面直角坐标系xOy中，直线y₁=ax+b与双曲线y₂= $\frac{k}{x}$ 交于A（1，3）和B（﹣3，﹣1）两点．
观察图像可知：
①当x=﹣3或1时，y₁=y₂；
②当﹣3＜x＜0或x＞1时，y₁＞y₂ ，即通过观察函数的图象，可以得到不等式ax+b＞ $\frac{k}{x}$ 的解集．
有这样一个问题：求不等式x³+4x²﹣x﹣4＞0的解集．
某同学根据学习以上知识的经验，对求不等式x³+4x²﹣x﹣4＞0的解集进行了探究．
下面是他的探究过程，请将（1）、（2）、（3）补充完整：

(1)、①将不等式按条件进行转化：
当x=0时，原不等式不成立；
当x＞0时，原不等式可以转化为x²+4x﹣1＞ $\frac{4}{x}$ ；
当x＜0时，原不等式可以转化为x²+4x﹣1＜ $\frac{4}{x}$ ；
②构造函数，画出图像
设y₃=x²+4x﹣1，y₄= $\frac{4}{x}$ ，在同一坐标系中分别画出这两个函数的图象．
双曲线y₄= $\frac{4}{x}$ 如图2所示，请在此坐标系中画出抛物线y₃=x²+4x﹣1；（不用列表）

(2)、确定两个函数图象公共点的横坐标
观察所画两个函数的图象，猜想并通过代入函数解析式验证可知：满足y₃=y₄的所有x的值为

(3)、借助图像，写出解集
结合（1）的讨论结果，观察两个函数的图象可知：不等式x³+4x²﹣x﹣4＞0的解集为

查看试题解析
27.
已知如图：抛物线y=x²﹣1与x轴交于A，B两点，与y轴交于点C．

(1)、求A，B，C三点的坐标．

(2)、过点A作AP∥CB交抛物线于点P，求四边形ACBP的面积．

查看试题解析
28.
如图，在直角坐标系中，O为坐标原点，二次函数y=x²+mx+2的图象与x轴的正半轴交于点A，与y轴的正半轴交交于点B，且OA：OB=1：2．设此二次函数图象的顶点为D．

(1)、求这个二次函数的解析式；

(2)、将△OAB绕点A顺时针旋转90°后，点B落到点C的位置．将上述二次函数图象沿y轴向上或向下平移后经过点C．请直接写出点C的坐标和平移后所得图象的函数解析式；

(3)、设（2）中平移后所得二次函数图象与y轴的交点为B₁ ，顶点为D₁ ．点P在平移后的二次函数图象上，且满足△PBB₁的面积是△PDD₁面积的2倍，求点P的坐标．

查看试题解析