2016-2017学年浙江省嘉兴市七校联考高一上学期期中数学试卷
试卷更新日期:2016-12-21 类型:期中考试
一、选择题
-
1. 已知集合A={x|x≤ },a=3,那么下列关系正确的是( )A、a⊆A B、a∈A C、a∉A D、{a}∈A2. 函数f(x)= 的定义域是( )A、(﹣∞,3) B、(3,+∞) C、(﹣∞,3)∩(3,+∞) D、(﹣∞,3)∪(3,+∞)3. 函数y= 的图象是( )A、
 B、
B、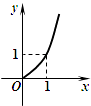 C、
C、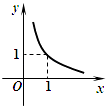 D、
D、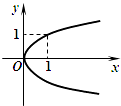 4. 函数f(x)=kx+b(k>0),若x∈[0,1],y∈[﹣1,1],则函数y=f(x)的解析式是( )A、y=2x﹣1 B、 C、y=2x﹣1或y=﹣2x+1 D、y=﹣2x﹣15. 0.32 , log20.3,20.3这三个数之间的大小顺序是( )A、0.32<20.3<log20.3 B、0.32<log20.3<20.3 C、log20.3<0.32<20.3 D、log20.3<20.3<0.326. 若f(x)=x ,则f(2)=( )A、3 B、﹣3 C、 D、-7. 函数y=ax在[0,1]上最大值与最小值的和为3,则a=( )A、2 B、 C、4 D、8. 已知f(x)是区间(﹣∞,+∞)上的偶函数,且是[0,+∞)上的减函数,则( )A、f(﹣3)<f(﹣5) B、f(﹣3)>f(﹣5) C、f(﹣3)<f(5) D、f(﹣3)=f(﹣5)9. 函数f(x)=ax﹣1+4(a>0,且a≠1)的图象过一个定点,则这个定点坐标是( )A、(5,1) B、(1,5) C、(1,4) D、(4,1)10. 若loga3<1,则a取值范围是( )A、a>3 B、1<a<3 C、0<a<1 D、a>3或0<a<111. 若增函数f(x)=ax+b与x轴交点是(2,0),则不等式bx2﹣ax>0的解集是( )A、 B、 C、 D、12. 若x∈(0, ]时,恒有4x<logax,则a的取值范围是( )A、 B、 C、 D、
4. 函数f(x)=kx+b(k>0),若x∈[0,1],y∈[﹣1,1],则函数y=f(x)的解析式是( )A、y=2x﹣1 B、 C、y=2x﹣1或y=﹣2x+1 D、y=﹣2x﹣15. 0.32 , log20.3,20.3这三个数之间的大小顺序是( )A、0.32<20.3<log20.3 B、0.32<log20.3<20.3 C、log20.3<0.32<20.3 D、log20.3<20.3<0.326. 若f(x)=x ,则f(2)=( )A、3 B、﹣3 C、 D、-7. 函数y=ax在[0,1]上最大值与最小值的和为3,则a=( )A、2 B、 C、4 D、8. 已知f(x)是区间(﹣∞,+∞)上的偶函数,且是[0,+∞)上的减函数,则( )A、f(﹣3)<f(﹣5) B、f(﹣3)>f(﹣5) C、f(﹣3)<f(5) D、f(﹣3)=f(﹣5)9. 函数f(x)=ax﹣1+4(a>0,且a≠1)的图象过一个定点,则这个定点坐标是( )A、(5,1) B、(1,5) C、(1,4) D、(4,1)10. 若loga3<1,则a取值范围是( )A、a>3 B、1<a<3 C、0<a<1 D、a>3或0<a<111. 若增函数f(x)=ax+b与x轴交点是(2,0),则不等式bx2﹣ax>0的解集是( )A、 B、 C、 D、12. 若x∈(0, ]时,恒有4x<logax,则a的取值范围是( )A、 B、 C、 D、二、填空题
-
13. 函数f(x)为(﹣∞,+∞)上的奇函数,则f(0)=14. 计算 = .
15. 已知函数f(x)= .则f(f(﹣1))= .16. 函数f(x)=x2﹣2ax+2在(﹣∞,6)内递减,则a的取值范围为 .17. 已知非空集合A={x∈R|x2<a2},B={x|1<x<3},若A∩B={x|1<x<2},则实数a的值为 .18. 已知f(x)在定义域(0,+∞)是单调函数,当x∈(0,+∞)时,都有f[f(x)﹣ ]=2,则f( )的值是 .三、解答题
-
19. 已知全集U=R,集合A={x|﹣1≤x≤3},B={x|x2<4},(1)、求A∪B;(2)、求集合∁UA.20. 计算:(lg ﹣lg25)÷100 .21. 已知函数f(x)=x﹣ ,(1)、判断函数f(x)的奇偶性;(2)、证明:f(x)在(0,+∞)上为单调增函数.22. 已知函数f(x)=log2(x+1)﹣2.(1)、若f(x)>0,求x的取值范围.(2)、若x∈(﹣1,3],求f(x)的值域.