福建省仙游县郊尾、枫亭五校教研小片区2016-2017学年七年级下学期数学期中考试试卷
试卷更新日期:2018-05-15 类型:期中考试
一、单选题
-
1. 如图,a∥b,∠1=120°,则∠2等于( )
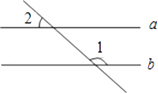 A、30° B、90° C、60° D、50°2. 在 ,2,0, 这四个数中,最小的数是( )A、-5 B、2 C、0 D、3. 如图,A,B,C,D中的图案( )可以通过如图平移得到.
A、30° B、90° C、60° D、50°2. 在 ,2,0, 这四个数中,最小的数是( )A、-5 B、2 C、0 D、3. 如图,A,B,C,D中的图案( )可以通过如图平移得到. A、
A、 B、
B、 C、
C、 D、
D、 4. 在实数3.14159, , ,π,0中,无理数有( )A、1个 B、2个 C、3个 D、4个5. 已知 是方程 的一个解,则 为( )A、2 B、-2 C、3 D、-36. 在平面直角坐标系中,点P(−1,m2+1)关于y轴的对称点P2一定在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限7. 一辆汽车在笔直的公路上行驶,两次拐弯后,仍在原来的方向上平行前进,如果汽车第一次右拐60°那么第二次拐弯应该( )A、左拐60° B、右拐60° C、左拐120° D、右拐120°8. 已知一个正数的两个平方根分别为 和 ,则这个正数为( )A、3 B、4 C、9 D、169. 某车间56名工人,每人每天能生产螺栓16个或螺母24个,设有x名工人生产螺栓,y名工人生产螺母,每天生产的螺栓和螺母按1:2配套,所列方程正确的是( )
4. 在实数3.14159, , ,π,0中,无理数有( )A、1个 B、2个 C、3个 D、4个5. 已知 是方程 的一个解,则 为( )A、2 B、-2 C、3 D、-36. 在平面直角坐标系中,点P(−1,m2+1)关于y轴的对称点P2一定在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限7. 一辆汽车在笔直的公路上行驶,两次拐弯后,仍在原来的方向上平行前进,如果汽车第一次右拐60°那么第二次拐弯应该( )A、左拐60° B、右拐60° C、左拐120° D、右拐120°8. 已知一个正数的两个平方根分别为 和 ,则这个正数为( )A、3 B、4 C、9 D、169. 某车间56名工人,每人每天能生产螺栓16个或螺母24个,设有x名工人生产螺栓,y名工人生产螺母,每天生产的螺栓和螺母按1:2配套,所列方程正确的是( )
A、 B、 C、 D、10. 由方程组 可以得出 的关系式是( )A、 B、 C、 D、二、填空题
-
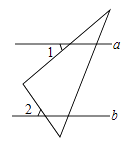
11. -8的立方根是.12. 在平面直角坐标系中,点P(-1,2)向右平移3个单位长度得到的点的坐标是 .13. P(m﹣4,1﹣m)在x轴上,则m= .14. 若 ,则 = .15. 已知直线a∥b,一块直角三角板如图所示放置,若∠1=37°,则∠2= .
 16. 三个同学对问题“若方程组 的解是 ,求方程组 的解.”提出各自的想法。甲说:“这个题目好像条件不够,不能求解”;乙说:“它们的系数有一定的规律,可以试试”;丙说:“能不能把第二个方程组的两个方程的两边都除以5,通过换元替换的方法来解决”.参考他们的讨论,你认为这个题目的解应该是 .
16. 三个同学对问题“若方程组 的解是 ,求方程组 的解.”提出各自的想法。甲说:“这个题目好像条件不够,不能求解”;乙说:“它们的系数有一定的规律,可以试试”;丙说:“能不能把第二个方程组的两个方程的两边都除以5,通过换元替换的方法来解决”.参考他们的讨论,你认为这个题目的解应该是 .
三、解答题
-
17. 计算:18. 解方程:19. 解方程组:20. 这是一个动物园游览示意图,如果以南门为坐标原点,东西为x轴,南北为y轴,
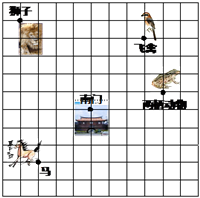 (1)、请按要求建立直角坐标系(2)、写出个动物园图中四个景点位置的坐标.21. 完成下面推理过程
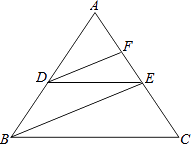
(1)、请按要求建立直角坐标系(2)、写出个动物园图中四个景点位置的坐标.21. 完成下面推理过程如图,已知DE∥BC,DF、BE分别平分∠ADE、∠ABC,可推得∠FDE=∠DEB的理由:
∵DE∥BC(已知)
∴∠ADE= . ()
∵DF、BE分别平分∠ADE、∠ABC,
∴∠ADF= ,
∠ABE= . ()
∴∠ADF=∠ABE
∴DF∥ . ()
∴∠FDE=∠DEB. ()
22. 如图,点E在DF上,点B在AC上, , .求证: ∥ .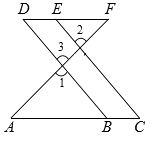 23. 已知关于 的二元一次方程组 的解满足 与 之和为2,求a的值.24. 在平面直角坐标系中,若点P(x,y)的坐标x、y均为整数,则称点P为格点.若一个多边形的面积记为S,其内部的格点数记为N,边界上的格点数记为L.例如图中△ABC是格点三角形,对应的S=1,N=0,L=4.
23. 已知关于 的二元一次方程组 的解满足 与 之和为2,求a的值.24. 在平面直角坐标系中,若点P(x,y)的坐标x、y均为整数,则称点P为格点.若一个多边形的面积记为S,其内部的格点数记为N,边界上的格点数记为L.例如图中△ABC是格点三角形,对应的S=1,N=0,L=4.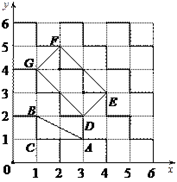 (1)、写出图中格点四边形DEFG对应的S,N,L.(2)、已知任意格点多边形的面积公式为S=N+aL+b,其中a,b为常数.当某格点多边形对应的N=82,L=38,求S的值.25. 某中学新建了一幢 层的教学大楼,每层楼有 间教室,进出这幢大楼一共有 道门,其中两道正门大小相同,两道侧门大小也相同,安全检查中,对 道门进行了测试,当同时开启一道正门和两道侧门时, 可以通过 名学生;当同时开启一道正门和一道侧门时, 可以通过 名学生。(1)、平均每分钟一道正门和一道侧门各可以通过多少名学生?(2)、检查中发现,紧急情况时因为学生拥挤,出门的效率将降低20%,安全检查规定,在紧急情况下,整幢教学大楼的学生应该在内通过这 道门安全撤离,假设这幢教学大楼每间教室最多有 名学生,则这幢教学大楼是否符合安全要求?请说明理由。26. 如图2,直线CB∥OA,∠B=∠A=108°,E、F在BC上,且满足 ,并且 平分 .
(1)、写出图中格点四边形DEFG对应的S,N,L.(2)、已知任意格点多边形的面积公式为S=N+aL+b,其中a,b为常数.当某格点多边形对应的N=82,L=38,求S的值.25. 某中学新建了一幢 层的教学大楼,每层楼有 间教室,进出这幢大楼一共有 道门,其中两道正门大小相同,两道侧门大小也相同,安全检查中,对 道门进行了测试,当同时开启一道正门和两道侧门时, 可以通过 名学生;当同时开启一道正门和一道侧门时, 可以通过 名学生。(1)、平均每分钟一道正门和一道侧门各可以通过多少名学生?(2)、检查中发现,紧急情况时因为学生拥挤,出门的效率将降低20%,安全检查规定,在紧急情况下,整幢教学大楼的学生应该在内通过这 道门安全撤离,假设这幢教学大楼每间教室最多有 名学生,则这幢教学大楼是否符合安全要求?请说明理由。26. 如图2,直线CB∥OA,∠B=∠A=108°,E、F在BC上,且满足 ,并且 平分 .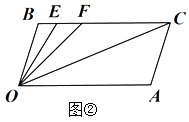 (1)、求 的度数;
(1)、求 的度数;
(2)、如图3,若平行移动AC,那么∠OCB:∠OFB的值是否随之发生变化?若变化,找出变化规律或求出变化范围;若不变,求出这个比值;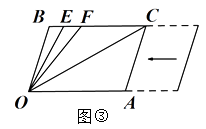 (3)、在平行移动AC的过程中,是否存在某种情况,使∠OEB=∠OCA?若存在,求出∠OCA的度数;若不存在,说明理由.
(3)、在平行移动AC的过程中,是否存在某种情况,使∠OEB=∠OCA?若存在,求出∠OCA的度数;若不存在,说明理由.