福建省南安市柳城义务教育小片区2016-2017学年七年级下学期数学期中考试试卷
试卷更新日期:2018-05-15 类型:期中考试
一、单选题
-
1. 若 是方程 的解,则a的值是( )A、5 B、2 C、1 D、-52. 下列方程中是二元一次方程的是( )A、 B、 C、 D、3. 方程2- 去分母得( )A、2-2(2x-4)=-(x-7) B、12-2(2x-4)=-x-7 C、12-4x-8=-(x-7) D、12-2(2x-4)=x-74. 已知x、y满足方程组 ,则x-y的值是( )A、-1 B、0 C、1 D、25. 已知a<b,则下列式子正确的是( )A、a+5>b+5 B、3a>3b C、-5a>-5b D、 >6. 不等式组 的解集在数轴上表示正确的是( )A、
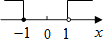 B、
B、 C、
C、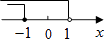 D、
D、 7. 商品按进价增加20%出售,因积压需降价处理,如果仍想获得8%的利润,则出售价需打( )A、9折 B、5折 C、8折 D、7.5折8. 不等式 的正整数解有( )A、1个 B、2个 C、3个 D、4个
7. 商品按进价增加20%出售,因积压需降价处理,如果仍想获得8%的利润,则出售价需打( )A、9折 B、5折 C、8折 D、7.5折8. 不等式 的正整数解有( )A、1个 B、2个 C、3个 D、4个二、填空题
-
9. 已知方程 ,用含 的代数式表示 ,则.10. 方程 的解是.11. 若 ,则 _ .12. x的 与5的差不小于3,用不等式表示为 .13. 请写出二元一次方程 在正整数范围内的所有解:.14. 已知 .①若 ,则 的取值范围是;②若 ,x-y=3,且 ,则 的取值范围是_.
三、解答题
-
15. 解方程:16. 解方程组:17. 解不等式 ,并把解集在数轴上表示出来.
 18. 已知二元一次方程组 的解也是方程 的解,求 的值.19. 学校准备添置一批课桌椅,原计划订购60套,每套100元.店方表示:如果多购可以优惠.结果校方购了72套,每套减价3元,但商店获得同样多的利润.求每套课桌椅的成本.20. 对于任意实数 、 ,定义一种新运算 ,其中a、b为常数,已知 , .(1)、求 和 的值;(2)、若 ,求 的取值范围.21. 已知关于 、 的方程组 的解满足 , .(1)、用含 的代数式分别表示 和 ;(2)、求 的取值范围;(3)、在 的取值范围内,当 为何整数时,不等式 的解为 ?22. 我们用 表示不大于 的最大整数,例如: , , ;用 表示大于 的最小整数,例如: , , .解决下列问题:(1)、 = , =;(2)、若 =2,则 的取值范围是;若 =-1,则 的取值范围是;(3)、已知 , 满足方程组 ,求 , 的取值范围.23. 小明到某服装商场进行社会调查,了解到该商场为了激励营业员的工作积极性,实行“月总收入=基本工资+计件奖金”的方法,并获得如下信息:
18. 已知二元一次方程组 的解也是方程 的解,求 的值.19. 学校准备添置一批课桌椅,原计划订购60套,每套100元.店方表示:如果多购可以优惠.结果校方购了72套,每套减价3元,但商店获得同样多的利润.求每套课桌椅的成本.20. 对于任意实数 、 ,定义一种新运算 ,其中a、b为常数,已知 , .(1)、求 和 的值;(2)、若 ,求 的取值范围.21. 已知关于 、 的方程组 的解满足 , .(1)、用含 的代数式分别表示 和 ;(2)、求 的取值范围;(3)、在 的取值范围内,当 为何整数时,不等式 的解为 ?22. 我们用 表示不大于 的最大整数,例如: , , ;用 表示大于 的最小整数,例如: , , .解决下列问题:(1)、 = , =;(2)、若 =2,则 的取值范围是;若 =-1,则 的取值范围是;(3)、已知 , 满足方程组 ,求 , 的取值范围.23. 小明到某服装商场进行社会调查,了解到该商场为了激励营业员的工作积极性,实行“月总收入=基本工资+计件奖金”的方法,并获得如下信息:营业员A:月销售件数200件,月总收入2400元;
营业员B:月销售件数300件,月总收入2700元;
假设营业员的月基本工资为 元,销售每件服装奖励 元.
(1)、求 、 的值;(2)、若某营业员的月总收入不低于3100元,那么他当月至少要卖服装多少件?(3)、商场为了多销售服装,对顾客推荐一种购买方式:如果购买甲3件,乙2件,丙1件共需350元;如果购买甲1件,乙2件,丙3件共需370元.某顾客想购买甲、乙、丙各一件共需多少元?