2016-2017学年江西省宜春三中高一上学期期中数学试卷
试卷更新日期:2016-12-21 类型:期中考试
一、选择题
-
1. 已知集合M={﹣1,0,1},则下列关系式正确的是( )A、{0}∈M B、{0}∉M C、0∈M D、0⊆M2. 已知函数f(x)=1+log2x,则 的值为( )A、 B、 C、0 D、﹣13. 函数y=(2k﹣1)x+b在(﹣∞,+∞)上是减函数,则( )A、 B、 C、 D、4. 与函数y=x相等的函数是( )A、y=( )2 B、y= C、y= D、y=5. 函数y=x2+2x﹣4,x∈[﹣2,2]的值域为( )A、[﹣5,4] B、[﹣4,4] C、[﹣4,+∞) D、(﹣∞,4]6. 若函数y=ax﹣1﹣2(a>0,且a≠1)的图像恒过点P,则点P为( )A、(0,﹣1) B、(0,﹣2) C、(1,﹣2) D、(1,﹣1)7. 下列式子中,成立的是( )A、log0.44>log0.46 B、1.013.4>1.013.5 C、3.50.3<3.40.3 D、log78<log878. 函数f(x)=﹣x3的图象关于( )A、y轴对称 B、直线y=﹣x对称 C、坐标原点对称 D、直线y=x对称9. 根据表格中的数据,可以判定方程ex﹣x﹣2=0的一个根所在的区间为( )
x
﹣1
0
1
2
3
ex
0.37
1
2.72
7.39
20.09
x+2
1
2
3
4
5
A、(﹣1,0) B、(0,1) C、(1,2) D、(2,3)10. 函数y=ax﹣ (a>0,a≠1)的图象可能是( )A、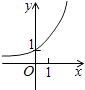 B、
B、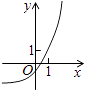 C、
C、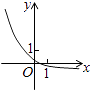 D、
D、 11. 若一系列函数的解析式和值域相同,但是定义域不同,则称这些函数为“同族函数”,例如函数y=x2 , x∈[1,2],与函数y=x2 , x∈[﹣2,﹣1]即为“同族函数”.下面的函数解析式也能够被用来构造“同族函数”的是( )A、y=x B、y=|x﹣3| C、y=2x D、y=log12. 若函数f(x)是偶函数,其定义域为(﹣∞,+∞),且在[0,+∞)上是减函数,则不等式f(lgx)>f(﹣1)成立的 x的取值范围为( )A、 B、 C、(0,10) D、(10,+∞)
11. 若一系列函数的解析式和值域相同,但是定义域不同,则称这些函数为“同族函数”,例如函数y=x2 , x∈[1,2],与函数y=x2 , x∈[﹣2,﹣1]即为“同族函数”.下面的函数解析式也能够被用来构造“同族函数”的是( )A、y=x B、y=|x﹣3| C、y=2x D、y=log12. 若函数f(x)是偶函数,其定义域为(﹣∞,+∞),且在[0,+∞)上是减函数,则不等式f(lgx)>f(﹣1)成立的 x的取值范围为( )A、 B、 C、(0,10) D、(10,+∞)二、填空题
-
13. 已知A={﹣1,3,m},集合B={3,5},若B∩A=B,则实数m= .14. 已知幂函数y=f(x)的图象过点(2, ),则f(x)= .15. 函数f(x)= 的定义域为 .16. 下列四个结论中:
(1)如果两个函数都是增函数,那么这两个函数的积运算所得函数为增函数;
(2)奇函数f(x)在[0,+∞)上是增函数,则f(x)在R上为增函数;
(3)既是奇函数又是偶函数的函数只有一个;
(4)若函数f(x)的最小值是a,最大值是b,则f(x)值域为[a,b].
其中正确结论的序号为 .
三、解答题
-
17. 已知集合A={x|3≤x≤7},B={x|3<2x﹣1<19},求:(1)、求A∪B;(2)、求(∁RA)∩B.18. 计算与解方程(1)、计算:(2 ) +(lg5)0+( ) ;(2)、解方程:log3(6x﹣9)=3.19. 已知函数f(x)=x2+bx+c,(1)、若函数f(x)是偶函数,求实数b的值(2)、若函数f(x)在区间[﹣1,3]上单调递增,求实数b的取值范围.20. 已知函数f(x)= .(1)、判断函数f(x)在区间[1,+∞)上的单调性,并用定义证明你的结论;(2)、求函数f(x)在区间[2,4]上的最大值与最小值.