2016-2017学年天津市南开区八年级上学期期中数学试卷
试卷更新日期：2016-12-20 类型：期中考试
一、选择题
-
1. 在以下绿色食品、回收、节能、节水四个标志中，是轴对称图形的是（ ）A、
B、
C、
D、
2. 下列四个等式从左到右的变形，是多项式因式分解的是（ ）A、（a+3）（a﹣3）=a2﹣9 B、x2+x﹣5=x（x+1）﹣5 C、x2+x=x（x+ ） D、a2b+ab2=ab（a+b）3. 下列运算正确的是（ ）A、﹣a（a﹣b）=﹣a2﹣ab B、（2ab）2+a2b=4ab C、2ab∙3a=6a2b D、（a﹣1）（1﹣a）=a2﹣14. 分解因式x2y﹣y3结果正确的是（ ）A、y（x+y）2 B、y（x﹣y）2 C、y（x2﹣y2） D、y（x+y）（x﹣y）5. 长方形的面积为4a2﹣6ab+2a，若它的一边长为2a，则它的周长为（ ）A、4a﹣3b B、8a﹣6b C、4a﹣3b+1 D、8a﹣6b+26. 如图，有A、B、C三个居民小区的位置成三角形，现决定在三个小区之间修建一个购物超市，使超市到三个小区的距离相等，则超市应建在（ ）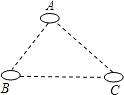
A、在AC，BC两边高线的交点处 B、在AC，BC两边中线的交点处 C、在AC，BC两边垂直平分线的交点处 D、在∠A，∠B两内角平分线的交点处7. 若（x+y）2=11，（x﹣y）2=7，则xy和（x2+y2）的值分别为（ ）A、4，18 B、1，18 C、1，9 D、4，98. 2016×2016﹣2016×2015﹣2015×2014+2015×2015的值为（ ）A、1 B、﹣1 C、4032 D、40319. 根据下列已知条件，能唯一画出△ABC的是（ ）A、AB=3，BC=4，AC=8 B、AB=4，BC=3，∠A=30° C、∠A=60°，∠B=45°，AB=4 D、∠C=90°，AB=610. 如图，已知△ABC中，AD=BD，AC=4，H是高AD和BE的交点，则线段BH的长度为（ ）
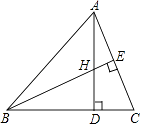A、 B、4 C、2 D、511. 如图，△ABC中，AB=AC，D是BC的中点，AC的垂直平分线分别交AC、AD、AB于点E、O、F，则图中全等三角形的对数是（ ）
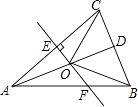A、1对 B、2对 C、3对 D、4对12. 如图，△ABE和△ADC分别沿着边AB，AC翻折180°形成的，若∠BCA：∠ABC：∠BAC=28：5：3，BE与DC交于点F，则∠EFC的度数为（ ）
A、20° B、30° C、40° D、45°二、填空题
-
13. 如果点P（﹣2，b）和点Q（a，﹣3）关于x轴对称，则a+b的值是 ．14. 如图，△ABC的周长为19cm，AC的垂直平分线DE交AC于点E，E为垂足，AE=3cm，则△ABD的周长为 ．
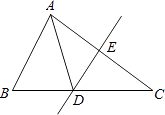15. 如图，AE∥DF，AB=DC，不再添加辅助线和字母，要使△EAC≌△FDB，需添加的一个条件是（只写一个条件即可）
16. 点O是△ABC内一点，且点O到三边的距离相等，∠A=50°，则∠BOC= ．17. 若x2﹣（m﹣1）x+36是一个完全平方式，则m的值为 ．18. 阅读下文，寻找规律．计算：（1﹣x）（1+x）=1﹣x2 ， （1﹣x）（1+x+x2）=1﹣x3 ， （1﹣x）（1+x+x2+x3）=1﹣x4…．
(1)、观察上式，并猜想：（1﹣x）（1+x+x2+…+xn）= ．(2)、根据你的猜想，计算：1+3+32+33…+3n= ． （其中n是正整数）三、解答题：
-
19. 在平面直角坐标系中，A（1，2），B（3，1），C（﹣2，﹣1）．
(1)、在图中作出△ABC关于y轴的对称△A1B1C1；(2)、写出△ABC关于x轴对称△A2B2C2的各顶点坐标：A2；
B2；
C2 ．
20. 化简求值：（2x﹣1）2﹣（3x+1）（3x﹣1）+5x（x﹣1），x=﹣ ．21. 因式分解：(1)、18axy﹣3ax2﹣27ay2(2)、（a2+4）2﹣16a2(3)、c（a﹣b）﹣2（a﹣b）2c+（a﹣b）3c．22. 如图，B是AC中点，∠F=∠E，∠1=∠2．证明：AE=CF．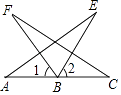
23. 已知：如图，∠BAC的角平分线与BC的垂直平分线DG交于点D，DE⊥AB，DF⊥AC，垂足分别为E，F．①求证：BE=CF；
②若AF=5，BC=6，求△ABC的周长．
24. 阅读
(1)、阅读理解：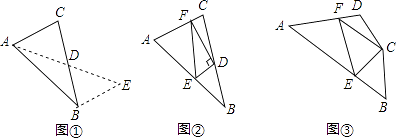
如图①，在△ABC中，若AB=10，AC=6，求BC边上的中线AD的取值范围．
解决此问题可以用如下方法：延长AD到点E使DE=AD，再连接BE（或将△ACD绕着点D逆时针旋转180°得到△EBD），把AB，AC，2AD集中在△ABE中，利用三角形三边的关系即可判断．
中线AD的取值范围是；
(2)、问题解决：如图②，在△ABC中，D是BC边上的中点，DE⊥DF于点D，DE交AB于点E，DF交AC于点F，连接EF，求证：BE+CF＞EF；
(3)、问题拓展：如图③，在四边形ABCD中，∠B+∠D=180°，CB=CD，∠BCD=140°，以C为顶点作一个70°角，角的两边分别交AB，AD于E，F两点，连接EF，探索线段BE，DF，EF之间的数量关系，并加以证明．