2016-2017学年山东省东营市八年级上学期期中数学试卷

试卷更新日期：2016-12-20 类型：期中考试

进入出卷网下载

一、选择题

1. 下列运算中，计算正确的是（）

A、2a•3a=6a B、（3a²）³=27a⁶ C、a⁴÷a²=2a D、（a+b）²=a²+ab+b²

查看试题解析
2. 下列各式的计算中，正确的是（）

A、 $\sqrt{(- 4) \times (- 9)} = \sqrt{- 4} \times \sqrt{(- 9)} = 6$ B、 $\sqrt{3^{2} + 4^{2}} = 3 + 4 = 7$ C、 $\sqrt{41^{2} - 40^{2}} = \sqrt{81} \times \sqrt{1} = 9$ D、 $3 \sqrt{\frac{2}{3}} = \sqrt{2}$

查看试题解析
3. 下列多项式中能用平方差公式分解因式的是（　　）

A、a²+（﹣b）² B、5m²﹣20mn C、﹣x²﹣y² D、﹣x²+9

查看试题解析
4. 已知a^m=9，a^m^﹣²ⁿ=3，则aⁿ的值是（）

A、﹣3 B、 $\sqrt{3}$ C、 $\frac{1}{3}$ D、± $\sqrt{3}$

查看试题解析
5. 若4x²﹣2（k﹣1）x+9是完全平方式，则k的值为（）

A、±2 B、±5 C、7或﹣5 D、﹣7或5

查看试题解析
6. 若（x﹣5）（x+3）=x²+mx﹣15，则（）

A、m=8 B、m=﹣8 C、m=2 D、m=﹣2

查看试题解析
7. 把根号外的因式化到根号内：﹣a $\sqrt{- a}$ =（）

A、 $\sqrt{- a^{2}}$ B、 $\sqrt{- a^{3}}$ C、﹣ $\sqrt{- a^{3}}$ D、 $\sqrt{a^{3}}$

查看试题解析
8. 计算 $(\frac{a^{2} + b^{2}}{a^{2} - b^{2}} - \frac{a - b}{a + b}) \times \frac{a - b}{2 a b}$ 的结果是（）

A、 $\frac{1}{a - b}$ B、 $\frac{1}{a + b}$ C、a﹣b D、a+b

查看试题解析
9. 如图，正方形卡片A类、B类和长方形卡片C类各若干张，如果要拼一个长为（a+3b），宽为（2a+b）的大长方形，则需要A类、B类和C类卡片的张数分别为（）

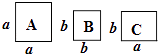A、2，3，7 B、3，7，2 C、2，5，3 D、2，5，7

查看试题解析
10. 计算 ${(\sqrt{2 - x})}^{2} + \sqrt{{(x - 3)}^{2}}$ 的结果是（）

A、1 B、﹣1 C、2x﹣5 D、5﹣2x

查看试题解析
11. 已知a= $\sqrt{5}$ +2，b= $\sqrt{5}$ ﹣2，则 $\sqrt{a^{2} + b^{2} + 7}$ 的值为（）

A、3 B、4 C、5 D、6

查看试题解析
12. 观察下列等式：a₁=n，a₂=1﹣ $\frac{1}{a_{1}}$ ，a₃=1﹣ $\frac{1}{a_{2}}$ ，a₄=1﹣ $\frac{1}{a_{3}}$ ，…根据其蕴含的规律可得（）

A、a₂₀₁₆=n B、a₂₀₁₆= $\frac{n - 1}{n}$ C、a₂₀₁₆= $\frac{1}{n - 1}$ D、a₂₀₁₆= $\frac{1}{1 - n}$

查看试题解析

二、填空题

13. 已知m＜0，那么| $\sqrt{m^{2}}$ ﹣2m|值为．

查看试题解析
14. 计算：（2 $\sqrt{2}$ ﹣3）²⁰¹⁵×（2 $\sqrt{2}$ +3）²⁰¹⁶= ．

查看试题解析
15. 一个长方形的面积为a²﹣4b² ，若一边长为2a+4b，则周长为．

查看试题解析
16. 已知2x+y﹣3=0，则2^y•4^x的值是．

查看试题解析
17. 已知a+b=﹣4，ab=2，则 $\sqrt{\frac{a}{b}} + \sqrt{\frac{b}{a}}$ 的值等于

查看试题解析
18. 若关于x的方程 $\frac{2}{x - 2}$ + $\frac{x + m}{2 - x}$ =2有增根，则m的值是．

查看试题解析
19. 已知 $\frac{a}{x + 2}$ 与 $\frac{b}{x - 2}$ 的和等于 $\frac{4 x}{x^{2} - 4}$ ，则 $\sqrt{a b}$ = ．

查看试题解析

三、计算题

20. 计算化简

(1)、10 $\sqrt{\frac{1}{5}}$ + $\frac{5}{2}$ $\sqrt{\frac{4}{5}}$ ﹣ $\sqrt{45}$

(2)、 $\sqrt{18}$ ÷（ $\frac{1}{\sqrt{3}}$ ﹣ $\frac{1}{\sqrt{6}}$ ）

(3)、（2x³y）²•（﹣2xy）+（﹣2x³y）³÷（2x²）

(4)、（ $\frac{1}{x - 2}$ ﹣1）÷ $\frac{x - 3}{x^{2} - 4}$ • $\frac{x}{x^{2} + 4 x + 4}$ ．

查看试题解析
21. 因式分解：

(1)、9（m+n）²﹣16（m﹣n）²；

(2)、（x+y）²﹣10（x+y）+25．

查看试题解析
22. 因式分解：

(1)、﹣12x²y+x³+36xy²

(2)、（x²y²+3）（x²y²﹣7）+25（实数范围内）．

查看试题解析
23. 先化简，再求值：
[（x﹣2y）²﹣（﹣x﹣2y）（﹣x+2y）]÷（﹣4y），其中x和y的取值满足 $\sqrt{x^{2} - 2 x + 1}$ +（x²+4xy+4y²）=0．

查看试题解析
24. 某同学在计算3（4+1）（4²+1）时，把3写成4﹣1后，发现可以连续运用两数和乘以这两数差公式计算：
3（4+1）（4²+1）=（4﹣1）（4+1）（4²+1）=（4²﹣1）（4²+1）=16²﹣1=255．
请借鉴该同学的经验，计算： $(1 + \frac{1}{2}) (1 + \frac{1}{2^{2}}) (1 + \frac{1}{2^{4}}) (1 + \frac{1}{2^{8}}) + \frac{1}{2^{15}}$ ．

查看试题解析
25. 若关于x的分式方程 $\frac{2 m + x}{x + 3}$ ﹣1= $\frac{2}{x}$ 无解，求m的值．

查看试题解析

四、解答题

26. 东营市某学校2015年在商场购买甲、乙两种不同足球，购买甲种足球共花费2000元，购买乙种足球共花费1400元，购买甲种足球数量是购买乙种足球数量的2倍，且购买一个乙种足球比购买一个甲种足球多花20元．

(1)、求购买一个甲种足球、一个乙种足球各需多少元；

(2)、2016年为响应习总书记“足球进校园”的号召，这所学校决定再次购买甲、乙两种足球共50个，恰逢该商场对两种足球的售价进行调整，甲种足球售价比第一次购买时提高了10%，乙种足球售价比第一次购买时降低了10%，如果此次购买甲、乙两种足球的总费用不超过2900元，那么这所学校最多可购买多少个乙种足球？

查看试题解析
27. 探索规律
观察下列各式及验证过程：n=2时，有式①： $2 \times \sqrt{\frac{2}{3}} = \sqrt{2 + \frac{2}{3}}$ ；n=3时，有式②： $3 \times \sqrt{\frac{3}{8}} = \sqrt{3 + \frac{3}{8}}$ ；
式①验证： $2 \times \sqrt{\frac{2}{3}} = \sqrt{\frac{2^{2}}{3}} = \sqrt{\frac{(2^{3} - 2) + 2}{2^{2} - 1}} = \sqrt{\frac{(2^{2} - 1) + 2}{2^{2} - 1}} = \sqrt{2 + \frac{2}{3}}$
式②验证： $3 \times \sqrt{\frac{3}{8}} = \sqrt{\frac{3^{3}}{8}} = \sqrt{\frac{(3^{3} - 3) + 3}{3^{2} - 1}} = \sqrt{\frac{3 (3^{2} - 3) + 3}{3^{2} - 1}}$ $= \sqrt{3 + \frac{3}{8}}$

(1)、针对上述式①、式②的规律，请写出n=4时的式子；

(2)、请写出满足上述规律的用n（n为任意自然数，且n≥2）表示的等式，并加以验证．

查看试题解析