2016-2017学年广西桂林市灌阳县八年级上学期期中数学试卷

试卷更新日期：2016-12-20 类型：期中考试

进入出卷网下载

一、选择题

1. 下列每组数分别表示三根木棒的长度，将它们首尾连接后，不能摆成三角形的一组是（）

A、2，3，5 B、3，4，6 C、4，5，7 D、5，6，8

查看试题解析
2. 用科学记数法表示0.00001032，下列正确的是（）

A、0.1032×10^﹣⁴ B、1.032×10³ C、10.32×10^﹣⁶ D、1.032×10^﹣⁵

查看试题解析
3. 分式方程 $\frac{2}{x + 1}$ = $\frac{1}{x - 1}$ 的解为（）

A、x=1 B、x=2 C、x=3 D、x=﹣1

查看试题解析
4. 如果把分式 $\frac{2 a + b}{2 a b}$ 中的a和b都扩大了2倍，那么分式的值（）

A、扩大2倍 B、不变 C、缩小2倍 D、缩小4倍

查看试题解析
5. 下列各式中，计算正确的是（）

A、3^﹣¹=﹣3 B、3^﹣³=﹣9 C、3^﹣²= $\frac{1}{9}$ D、3⁰=0

查看试题解析
6. 下列语句中，不是命题的是（）

A、锐角小于钝角 B、作∠A的平分线 C、对顶角相等 D、同角的补角相等

查看试题解析
7. 如图，已知∠1=∠2，要得到△ABD≌△ACD，还需从下列条件中补选一个，则错误的选法是（）

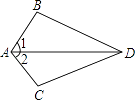A、AB=AC B、DB=DC C、∠ADB=∠ADC D、∠B=∠C

查看试题解析
8. 如图，在△ACB中，∠ACB=100°，∠A=20°，D是AB上一点．将△ABC沿CD折叠，使B点落在AC边上的B′处，则∠ADB′等于（）

A、25° B、30° C、35° D、40°

查看试题解析
9. 下列分式不是最简分式的是（）

A、 $\frac{3 x}{3 x + 1}$ B、 $\frac{x - y}{x^{2} + y^{2}}$ C、 $\frac{x^{2} - y}{x^{2} - x y + y^{2}}$ D、 $\frac{6 x}{4 y}$

查看试题解析
10. △ABC是不规则三角形，若线段AD把△ABC分为面积相等的两部分，则线段AD应该是（）

A、三角形的角平分线 B、三角形的中线 C、三角形的高 D、以上都不对

查看试题解析
11. 两个角的两边分别平行，那么这两个角（）

A、相等 B、互补 C、互余 D、相等或互补

查看试题解析
12. 如图，△ABC中，∠A=α°，BO，CO分别是∠ABC，∠ACB的平分线，则∠BOC的度数是（）

A、2α° B、（α+60）° C、（α+90）° D、（ $\frac{1}{2}$ α+90）°

查看试题解析

二、填空题

13. 若分式 $\frac{3 x - 6}{2 x + 1}$ 的值为0，则x= ．

查看试题解析
14. 已知 $\frac{x + 2}{x - 2}$ ﹣（x﹣1）⁰有意义，则x的取值范围是．

查看试题解析
15. 如图所示，在△ABC中，AB=5，BC=7，将△ABC折叠，使点C与点A重合，折痕为DE，则△ABE的周长为．

查看试题解析
16. 如图，已知AF∥EC，AB∥CD，∠A=65°，则∠C=度．

查看试题解析
17. 已知点D是△ABC的边AB上一点，且AD=BD=CD，则∠ACB=度．

查看试题解析
18.
广场要做一个由若干盆花组成的形如正六边形的花坛，每条边（包括两个顶点）有n（n＞1）盆花，设这个花坛边上的花盆的总数为S，请观察图中的规律：
按上规律推断，S与n的关系是．

查看试题解析

三、解答题

19. 计算：

(1)、3a²b³÷ $\frac{2}{3}$ a³b• $\frac{3}{2}$ ab³

(2)、（ $\frac{x z^{2}}{- y}$ ）³（ $\frac{y^{2}}{x z}$ ）⁴÷（ $\frac{x y}{- 2 x}$ ）³ ．

查看试题解析
20. 解方程：

(1)、 $\frac{2}{x - 2}$ ﹣ $\frac{3 x}{2 - x}$ =1

(2)、 $\frac{14}{x + 8}$ = $\frac{4}{x}$ + $\frac{10}{3 x + 24}$ ．

查看试题解析
21. 先化简再求值： $\frac{a - 1}{a - 2} \div \frac{a^{2} - 2 a + 1}{2 a - 4}$ ，其中a=﹣1．

查看试题解析
22. 符号“ $| \begin{matrix} a & b \\ c & d \end{matrix} |$ ”称为二阶行列式，规定它的运算法则为： $| \begin{matrix} a & b \\ c & d \end{matrix} |$ =ad﹣bc，请你根据上述规定求出下列等式中x的值． $| \begin{matrix} 2 & 1 \\ \frac{1}{x - 1} & \frac{1}{x - 1} \end{matrix} |$ =1

查看试题解析
23. 如图，AB=DE，AC=DF，BE=CF．求证：AB∥DE．

查看试题解析
24. 如图，△ABC中，∠ACB=90°，AD平分∠BAC，DE⊥AB于E．
求证：直线AD是线段CE的垂直平分线．

查看试题解析
25. 在一次“手拉手”捐款活动中，某同学对甲．乙两班捐款的情况进行统计，得到如下三条信息：
信息一．甲班共捐款120元，乙班共捐款88元；
信息二．乙班平均每人捐款数比甲班平均每人捐款数的0.8倍；
信息三．甲班比乙班多5人．
请你根据以上三条信息，求出甲班平均每人捐款多少元？

查看试题解析
26. 如图，已知△ABC中，AB=AC，∠BAC=90°，分别过B，C向过点A的直线作垂线，垂足分别为点E，F．

(1)、如图（1），过A的直线与斜边BC不相交时，求证：①△ABE≌△CAF； ②EF=BE+CF

(2)、如图（2），过A的直线与斜边BC相交时，其他条件不变，若BE=10，CF=3，试求EF的长．

查看试题解析