2018年中考数学专题高分攻略6讲专题二开放探索型问题
试卷更新日期：2018-05-11 类型：二轮复习
一、单选题
-
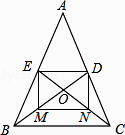
1. 如图，在正方形ABCD中，点E，F分别在BC，CD上，且∠EAF=45°，将△ABE绕点A顺时针旋转90°，使点E落在点E'处，则下列判断不正确的是（ ）
A、△AEE′是等腰直角三角形 B、AF垂直平分EE' C、△E′EC∽△AFD D、△AE′F是等腰三角形二、填空题
-
2.
如图，BC//EF，AC//DF，添加一个条件 ， 使得△ABC≌△DEF．
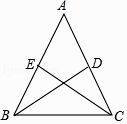
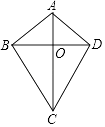
3. 如图，在四边形ABCD中，AB=AD，CB=CD，对角线AC，BD相交于点O，下列结论中：①∠ABC=∠ADC；
②AC与BD相互平分；
③AC，BD分别平分四边形ABCD的两组对角；
④四边形ABCD的面积S= AC•BD．
正确的是（填写所有正确结论的序号）
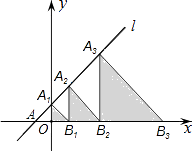
4.如图，在平面直角坐标系中，直线l：y=x+2交x轴于点A，交y轴于点A1 ， 点A2 ， A3 ， …在直线l上，点B1 ， B2 ， B3 ， …在x轴的正半轴上，若△A1OB1 ， △A2B1B2 ， △A3B2B3 ， …，依次均为等腰直角三角形，直角顶点都在x轴上，则第n个等腰直角三角形AnBn﹣1Bn顶点Bn的横坐标为 ．
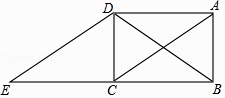
5. 如图，点B、F、C、E在一条直线上，已知FB=CE，AC∥DF，请你添加一个适当的条件使得△ABC≌△DEF．
6. 如图，四条直线l1：y1= x，l2：y2= x，l3：y3=﹣ x，l4：y4=﹣ x，OA1=1，过点A1作A1A2⊥x轴，交l1于点A2 ， 再过点A2作A2A3⊥l1交l2于点A3 ， 再过点A3作A3A4⊥l2交y轴于点A4…，则点A2017坐标为 ．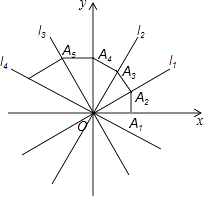
7. 庄子说：“一尺之椎，日取其半，万世不竭”．这句话（文字语言）表达了古人将事物无限分割的思想，用图形语言表示为图1，按此图分割的方法，可得到一个等式（符号语言）：1= + + +…+ +…．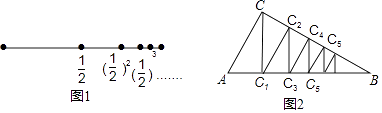
图2也是一种无限分割：在△ABC中，∠C=90°，∠B=30°，过点C作CC1⊥AB于点C1 ， 再过点C1作C1C2⊥BC于点C2 ， 又过点C2作C2C3⊥AB于点C3 ， 如此无限继续下去，则可将利△ABC分割成△ACC1、△CC1C2、△C1C2C3、△C2C3C4、…、△Cn﹣2Cn﹣1Cn、…．假设AC=2，这些三角形的面积和可以得到一个等式是 ．
三、综合题
-
