2016-2017学年新疆兵团四师七十一中九年级上学期期中数学试卷
试卷更新日期：2016-12-17 类型：期中考试
一、选择题
-
1. 已知x=2是一元二次方程x2﹣mx+2=0的一个解，则m的值是（ ）A、﹣3 B、3 C、0 D、0或32. 如图，晚上小亮在路灯下散步，在小亮由A处走到B处这一过程中，他在地上的影子（ ）
A、逐渐变短 B、逐渐变长 C、先变短后变长 D、先变长后变短3. 如图，在△ABC中，∠ABC和∠ACB的平分线交于点E，过点E作MN∥BC交AB于M，交AC于N，若BM+CN=9，则线段MN的长为（ ）
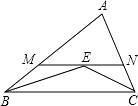A、6 B、7 C、8 D、94. 已知实数x，y满足 ，则以x，y的值为两边长的等腰三角形的周长是（ ）A、20或16 B、20 C、16 D、以上答案均不对5. 用配方法解关于x的一元二次方程x2﹣2x﹣3=0，配方后的方程可以是（ ）A、（x﹣1）2=4 B、（x+1）2=4 C、（x﹣1）2=16 D、（x+1）2=166. 在反比例函数 的图象上有两点（﹣1，y1）， ，则y1﹣y2的值是（ ）A、负数 B、非正数 C、正数 D、不能确定7. 已知等腰△ABC中，AD⊥BC于点D，且AD=BC，则△ABC底角的度数为（ ）A、45° B、75° C、45°或15°或75° D、60°8. 如图，在菱形ABCD中，∠A=60°，E，F分别是AB，AD的中点，DE，BF相交于点G，连接BD，CG．有下列结论：①∠BGD=120°；②BG+DG=CG；③△BDF≌△CGB；④S△ABD= AB2
其中正确的结论有（ ）
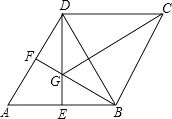A、1个 B、2个 C、3个 D、4个二、填空题
-
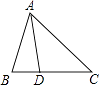
9. 方程x2﹣9=0的解是 ．10. 一元二次方程x2+2x+a=0有实根，则a的取值范围是 ．11. 平行四边形ABCD中，∠A+∠C=100°，则∠B=度．12. 如图，在△ABC中，AB=AD=DC，∠BAD=20°，则∠C= ．
13. 如图，正方形ABOC的边长为2，反比例函数y= 过点A，则k的值是 ．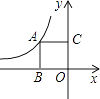
14. 如图，已知菱形ABCD的对角线AC、BD的长分别为6cm、8cm，AE⊥BC于点E，则AE的长是 ．
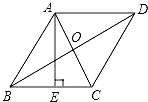15. 如图，边长12的正方形ABCD中，有一个小正方形EFGH，其中E，F，G分别在AB，BC，FD上．若BF=3，则小正方形的边长为 ．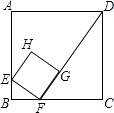
三、解答题
-
16. 解方程：(1)、2（x﹣3）=3x（x﹣3）；(2)、x2﹣2x=2x+1．17. 如图，在△ABC中，AB=AC，∠ABC=72°．
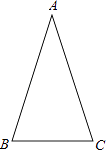(1)、用直尺和圆规作∠ABC的平分线BD交AC于点D（保留作图痕迹，不要求写作法）；(2)、在（1）中作出∠ABC的平分线BD后，求∠BDC的度数．18. 如图，已知AC⊥BC，BD⊥AD，AC与BD交于O，AC=BD．
求证：
(1)、BC=AD；(2)、△OAB是等腰三角形．19. 如图，路灯下一墙墩（用线段AB表示）的影子是BC，小明（用线段DE表示）的影子是EF，在M处有一颗大树，它的影子是MN．
(1)、指定路灯的位置（用点P表示）；(2)、在图中画出表示大树高的线段；(3)、若小明的眼睛近似地看成是点D，试画图分析小明能否看见大树．20. 如图，在矩形ABCD中，对角线BD的垂直平分线MN与AD相交于点M，与BC相交于点N，连接BM，DN．
(1)、求证：四边形BMDN是菱形；(2)、若AB=4，AD=8，求MD的长．21. 山西特产专卖店销售核桃，其进价为每千克40元，按每千克60元出售，平均每天可售出100千克，后来经过市场调查发现，单价每降低2元，则平均每天的销售可增加20千克，若该专卖店销售这种核桃要想平均每天获利2240元，请回答：(1)、每千克核桃应降价多少元？(2)、在平均每天获利不变的情况下，为尽可能让利于顾客，赢得市场，该店应按原售价的几折出售？22.一位同学拿了两块45°的三角尺△MNK，△ACB做了一个探究活动：将△MNK的直角顶点M放在△ABC的斜边AB的中点处，设AC=BC=a．
(1)、如图1，两个三角尺的重叠部分为△ACM，则重叠部分的面积为 ， 周长为；(2)、将图1中的△MNK绕顶点M逆时针旋转45°，得到图2，此时重叠部分的面积为 ， 周长为；(3)、如果将△MNK绕M旋转到不同于图1，图2的位置，如图3所示，猜想此时重叠部分的面积为多少？并试着加以验证．23.如图，已知反比例函数 的图象经过第二象限内的点A（﹣1，m），AB⊥x轴于点B，△AOB的面积为2．若直线y=ax+b经过点A，并且经过反比例函数 的图象上另一点C（n，一2）．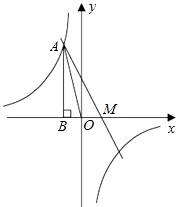
(1)、求直线y=ax+b的解析式；(2)、设直线y=ax+b与x轴交于点M，求AM的长．