2016-2017学年天津市武清区九年级上学期期中数学试卷

试卷更新日期：2016-12-17 类型：期中考试

进入出卷网下载

一、选择题

1. 一元二次方程3x²﹣4=﹣2x的二次项系数、一次项系数、常数项分别为（）

A、3，﹣4，﹣2 B、3，﹣2，﹣4 C、3，2，﹣4 D、3，﹣4，0

查看试题解析
2. 下列图形中，是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 抛物线y=（x+2）²+3的顶点坐标是（）

A、（﹣2，3） B、（2，3） C、（﹣2，﹣3） D、（2，﹣3）

查看试题解析
4. 下列方程是一元二次方程的是（）

A、x²+ $\frac{1}{x^{2}}$ =3 B、x²+x=y C、（x﹣4）（x+2）=3 D、3x﹣2y=0

查看试题解析
5. 如图，在△ABC中，∠C=90°，AC=4，BC=3，将△ABC绕点A逆时针旋转，使点C落在线段AB上的点E处，点B落在点D处，则B、D两点间的距离为（）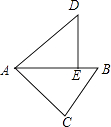

A、 $\sqrt{10}$ B、2 $\sqrt{2}$ C、3 D、2 $\sqrt{5}$

查看试题解析
6. 用配方法解一元二次方程ax²+bx+c=0（a≠0），此方程可变形为（）

A、（x+ $\frac{b}{2 a}$ ）²= $\frac{b^{2} - 4 a c}{4 a^{2}}$ B、（x+ $\frac{b}{2 a}$ ）²= $\frac{4 a c - b^{2}}{4 a^{2}}$ C、（x﹣ $\frac{b}{2 a}$ ）²= $\frac{b^{2} - 4 a c}{4 a^{2}}$ D、（x﹣ $\frac{b}{2 a}$ ）²= $\frac{4 a c - b^{2}}{4 a^{2}}$

查看试题解析
7. 已知函数y=ax²﹣2ax﹣1（a是常数，a≠0），下列结论正确的是（）

A、当a=1时，函数图象过点（﹣1，1） B、当a=﹣2时，函数图象与x轴没有交点 C、若a＞0，则当x≥1时，y随x的增大而减小 D、若a＜0，则当x≤1时，y随x的增大而增大

查看试题解析
8. 如图，将等边△ABC绕点C顺时针旋转120°得到△EDC，连接AD，BD．则下列结论：
①AC=AD；②BD⊥AC；③四边形ACED是菱形．
其中正确的个数是（）

A、0 B、1 C、2 D、3

查看试题解析
9. 已知（﹣1，y₁），（﹣2，y₂），（﹣4，y₃）是抛物线y=﹣2x²﹣8x+m上的点，则（　　）

A、y₁＜y₂＜y₃ B、y₃＜y₂＜y₁ C、y₃＜y₁＜y₂ D、y₂＜y₃＜y₁

查看试题解析
10. 电脑病毒传播快，如果一台电脑被感染，经过两轮感染后就会有81台电脑被感染．若每轮感染中平均一台电脑会感染x台电脑，则下面所列方程中正确的是（）

A、x（x+1）=81 B、1+x+x²=81 C、（1+x）²=81 D、1+（1+x）²=81

查看试题解析
11. 如图，已知二次函数y=ax²+bx+c（a≠0）的图象与x轴交于点A（﹣1，0），与y轴的交点B在（0，﹣2）和（0，﹣1）之间（不包括这两点），对称轴为直线x=1．下列结论：
①abc＞0
②4a+2b+c＞0
③4ac﹣b²＜8a
④ $\frac{1}{3}$ ＜a＜ $\frac{2}{3}$
⑤b＞c．
其中含所有正确结论的选项是（）

A、①③ B、①③④ C、②④⑤ D、①③④⑤

查看试题解析

二、填空题

12. 已知x=1是方程x²+mx+3=0的一个实数根，则m的值是．

查看试题解析
13. 如图所示的花朵图案，至少要旋转度后，才能与原来的图形重合．

查看试题解析
14. 如果关于x的一元二次方程x²+2ax+a+2=0有两个相等的实数根，那么实数a的值为

查看试题解析
15. 方程ax²+bx+c=0（a≠0）的两根为﹣3和1，那么抛物线y=ax²+bx+c（a≠0）的对称轴是直线．

查看试题解析
16. 一位运动员投掷铅球，如果铅球运行时离地面的高度为y（米）关于水平距离x（米）的函数解析式为y=﹣ $x^{2} + \frac{2}{3} x + \frac{5}{3}$ ，那么铅球运动过程中最高点离地面的距离为米．

查看试题解析
17. 如图，正方形ABCD绕点B逆时针旋转30°后得到正方形BEFG，EF与AD相交于点H，延长DA交GF于点K．若正方形ABCD边长为 $\sqrt{3}$ ，则AK= ．

查看试题解析

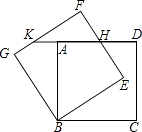
三、解答题

18. 解下列方程：

(1)、x²﹣2x=4

(2)、x（x﹣3）=x﹣3．

查看试题解析
19. 如图，在平面直角坐标系中，Rt△ABC的三个顶点分别是A（﹣4，2）、B（0，4）、C（0，2），

(1)、画出△ABC关于点C成中心对称的△A₁B₁C；平移△ABC，若点A的对应点A₂的坐标为（0，﹣4），画出平移后对应的△A₂B₂C₂；

(2)、△A₁B₁C和△A₂B₂C₂关于某一点成中心对称，则对称中心的坐标为．

查看试题解析
20. 已知二次函数y=﹣x²+2x+3．

(1)、求函数图象的顶点坐标和图象与x轴交点坐标；

(2)、当x取何值时，函数值最大？

(3)、当y＞0时，请你写出x的取值范围．

查看试题解析
21. 果农李明种植的草莓计划以每千克15元的单价对外批发销售，由于部分果农盲目扩大种植，造成该草莓滞销．李明为了加快销售，减少损失，对价格经过两次下调后，以每千克9.6元的单价对外批发销售．

(1)、求李明平均每次下调的百分率；

(2)、小刘准备到李明处购买3吨该草莓，因数量多，李明决定再给予两种优惠方案以供其选择：
方案一：打九折销售；
方案二：不打折，每吨优惠现金400元．试问小刘选择哪种方案更优惠，请说明理由．

查看试题解析
22. 如图，在正方形ABCD中，E，F是对角线BD上两点，且∠EAF=45°，将△ADF绕点A顺时针旋转90°后，得到△ABQ，连接EQ，求证：

(1)、EA是∠QED的平分线；

(2)、EF²=BE²+DF² ．

查看试题解析
23. 如图，某市近郊有一块长为60米，宽为50米的矩形荒地，地方政府准备在此建一个综合性休闲广场，其中阴影部分为通道，通道的宽度均相等，中间的三个矩形（其中三个矩形的一边长均为a米）区域将铺设塑胶地面作为运动场地．

(1)、设通道的宽度为x米，则a=（用含x的代数式表示）；

(2)、若塑胶运动场地总占地面积为2430平方米．请问通道的宽度为多少米？

查看试题解析
24.
如图1，抛物线y=﹣x²+bx+c与x轴交于A（2，0），B（﹣4，0）两点．

(1)、求该抛物线的解析式；

(2)、若抛物线交y轴于C点，在该抛物线的对称轴上是否存在点Q，使得△QAC的周长最小？若存在，求出Q点的坐标；若不存在，请说明理由．

(3)、在抛物线的第二象限图象上是否存在一点P，使得△PBC的面积最大？若存在，求出点P的坐标及△PBC的面积最大值；若不存，请说明理由．

查看试题解析