2016-2017学年江西省宜春三中九年级上学期期中数学试卷
试卷更新日期：2016-12-17 类型：期中考试
一、选择题
-
1. 下列安全标志图中，是中心对称图形的是（ ）A、
B、
C、
D、
2. 一元二次方程x2﹣1=0的根是（ ）A、1 B、﹣1 C、 D、±13. 用配方法解方程x2+8x﹣9=0时，此方程可变形为（ ）A、（x+4）2=7 B、（x+4）2=25 C、（x+4）2=9 D、（x+4）2=﹣74. 如图，把菱形ABOC绕点O顺时针旋转得到菱形DFOE，则下列角中不是旋转角的为（ ）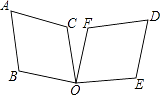
A、∠BOF B、∠AOD C、∠COE D、∠COF5. 根据下列表格的对应值，判断方程ax2+bx+c=0（a≠0，a、b、c为常数）一个解的范围是（ ）x
3.23
3.24
3.25
3.26
ax2+bx+c
﹣0.06
﹣0.02
0.03
0.09
A、3＜x＜3.23 B、3.23＜x＜3.24 C、3.24＜x＜3.25 D、3.25＜x＜3.266. 将抛物线y=3x2向左平移2个单位，再向下平移1个单位，所得抛物线为（ ）A、y=3（x﹣2）2﹣1 B、y=3（x﹣2）2+1 C、y=3（x+2）2﹣1 D、y=3（x+2）2+1二、填空题
-
7. 若x=2是一元二次方程x2﹣2a=0的一个根，则a= ．8. 在直角坐标系中，点A（1，﹣2）关于原点对称的点的坐标是 ．9. 抛物线y=x2﹣2x﹣8与x轴的交点坐标是 ．10. 将两块直角三角尺的直角顶点重合为如图的位置，若∠AOD=110°，则∠COB=度．
11. 如图所示，在直角坐标系中，△A′B′C′是由△ABC绕点P旋转一定的角度而得，其中A（1，4），B（0，2），C（3，0），则旋转中心点P的坐标是 ．
12. 如图，正方形ABCD与正三角形AEF的顶点A重合，将△AEF绕顶点A旋转，在旋转过程中，当BE=DF时，∠BAE的大小可以是 ．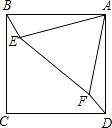
三、解答题
-
13. 解方程：2x2﹣4x+1=0．14. 已知抛物线l1的最高点为P（3，4），且经过点A（0，1），求l1的解析式．15. 随着市民环保意识的增强，烟花爆竹销售量逐年下降．常德市2012年销售烟花爆竹20万箱，到2014年烟花爆竹销售量为9.8万箱．求常德市2012年到2014年烟花爆竹年销售量的平均下降率．16. 已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，该抛物线与x轴的一个交点为（﹣1，0），请回答以下问题．
(1)、求抛物线与x轴的另一个交点坐标；(2)、一元二次方程ax2+bx+c=0（a≠0）的解为；(3)、不等式ax2+bx+c＜0（a≠0）的解集是 ．17. 如图，△ABC是直角三角形，延长AB到点E，使BE=BC，在BC上取一点F，使BF=AB，连接EF，△ABC旋转后能与△FBE重合，请回答：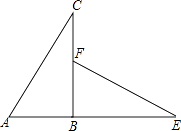
(1)、旋转中心是点 ， 旋转的最小角度是度(2)、AC与EF的位置关系如何，并说明理由．18. 已知关于x的一元二次方程kx2﹣2x+1=0．(1)、若此一元二次方程有实数根，求k的取值范围．(2)、选一个你认为合适的整数k代入原方程，并解此方程．19. 如图，在平面直角坐标系中，△ABC的三个顶点都在格点上，
(1)、①画出△ABC关于x轴对称的△A1B1C1 ．②画出△ABC绕原点O旋转180°后的△A2B2C2 ， 并写出A2、B2、C2的坐标
(2)、假设每个正方形网格的边长为1，求△A1B1C1的面积．20. 已知二次函数y=2x2+bx﹣1．(1)、若两点P（﹣3，m）和Q（1，m）在该函数图象上．求b、m的值；(2)、设该函数的顶点为点B，求出点B 的坐标并求三角形BPQ的面积．21. 某商品的进价为每件20元，售价为每件25元时，每天可卖出250件．市场调查反映：如果调整价格，一件商品每涨价1元，每天要少卖出10件．(1)、求出每天所得的销售利润w（元）与每件涨价x（元）之间的函数关系式；并写出自变量的取值范围(2)、商场的营销部在调控价格方面，提出了A，B两种营销方案．方案A：每件商品涨价不超过11元；
方案B：每件商品的利润至少为16元．
请比较哪种方案的最大利润更高，并说明理由．
22. 如图，平行四边形ABCD中，AB⊥AC，AB=1，BC= ．对角线AC，BD相交于点O，将直线AC绕点O顺时针旋转，分别交BC，AD于点E，F．
(1)、证明：当旋转角为90°时，四边形ABEF是平行四边形；(2)、试说明在旋转过程中，线段AF与EC总保持相等；(3)、在旋转过程中，四边形BEDF可能是菱形吗？如果不能，请说明理由；如果能，说明理由并求出此时AC绕点O顺时针旋转的度数．23.如图，抛物线y=﹣x2+mx+n与x轴交于A，B两点，y与轴交于点C，抛物线的对称轴交x轴于点D．已知A（﹣1，0），C（0，3）
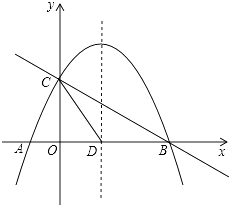(1)、求抛物线的解析式；(2)、在抛物线的对称轴上是否存在P点，使△PCD是以CD为腰的等腰三角形，如果存在，直接写出点P的坐标，如果不存在，请说明理由；(3)、点E是线段BC上的一个动点，过点E作x轴的垂线与抛物线相交于点F，①求直线BC 的解析式；
②当点E运动到什么位置时，四边形CDBF的面积最大？求四边形CDBF的最大面积及此时点E的坐标．