河北省保定市2018届高三文数第一次模拟考试试卷
试卷更新日期:2018-05-08 类型:高考模拟
一、单选题
-
1. 已知集合 ,集合 ,则 的子集个数为( )A、1 B、2 C、3 D、42. 设 为 的虚部, 为 的实部,则 ( )A、-1 B、-2 C、-3 D、03. 已知具有线性相关的变量 ,设其样本点为 ,回归直线方程为 ,若 ,( 为原点),则 ( )
A、 B、 C、 D、4. 已知非向量 ,则 或 是向量 与 夹角为锐角的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件5. 已知 ,则 为( )A、 B、 C、 D、6. 2002年国际数学家大会在北京召开,会标是以我国古代数学家赵爽的弦图为基础设计.弦图是由四个全等的直角三角形与一个小正方形拼成的一个大正方形(如图).如果小正方形的边长为2,大正方形的边长为10,直角三角形中较小的锐角为 ,则 ( )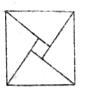 A、 B、 C、 D、7. 如图所示的程序框图中,输出的 为 ( )
A、 B、 C、 D、7. 如图所示的程序框图中,输出的 为 ( )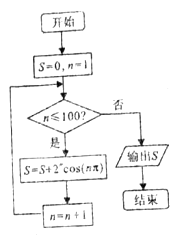 A、 B、 C、 D、8. 已知函数 既是二次函数又是幂函数,函数 是 上的奇函数,函数 ,则 ( )A、0 B、2018 C、4036 D、40379. 如图是某几何体的三视图,则该几何体的表面积为( )
A、 B、 C、 D、8. 已知函数 既是二次函数又是幂函数,函数 是 上的奇函数,函数 ,则 ( )A、0 B、2018 C、4036 D、40379. 如图是某几何体的三视图,则该几何体的表面积为( ) A、 B、 C、 D、10. 已知向量 ,向量 ,函数 ,则下列说法正确的是( )A、 是奇函数 B、 的一条对称轴为直线 C、 的最小正周期为 D、 在 上为减函数11. 已知双曲线 的左顶点为 ,虚轴长为8,右焦点为 ,且 与双曲线的渐近线相切,若过点 作 的两条切线,切点分别为 ,则 ( )A、8 B、 C、 D、12. 定义在 上的偶函数 满足 ,当 时, ,设函数 ,则函数 与 的图象所有交点的横坐标之和为( )A、2 B、4 C、6 D、8
A、 B、 C、 D、10. 已知向量 ,向量 ,函数 ,则下列说法正确的是( )A、 是奇函数 B、 的一条对称轴为直线 C、 的最小正周期为 D、 在 上为减函数11. 已知双曲线 的左顶点为 ,虚轴长为8,右焦点为 ,且 与双曲线的渐近线相切,若过点 作 的两条切线,切点分别为 ,则 ( )A、8 B、 C、 D、12. 定义在 上的偶函数 满足 ,当 时, ,设函数 ,则函数 与 的图象所有交点的横坐标之和为( )A、2 B、4 C、6 D、8二、填空题
-
13. 抛物线的顶点在原点,焦点在 轴上,抛物线上的点 到焦点的距离为3,则14. 甲、乙、丙三个各自独立地做同一道数学题,当他们都把自己的答案公布出来之后,
甲说:我做错了;
乙说:丙做对了;
丙说:我做错了.
在一旁的老师看到他们的答案并听取了他们的意见后说:“你们三个人中有一个人做对了,有一个说对了.”
请问他们三个人中做对了的是
15. 已知实数 满足 ,若 取得最小值时的最优解 满足 ,则 的最小值为16. 已知 分别为 的三个内角 的对边, ,且 ,则三、解答题
-
17. 已知数列 满足: ,且 .(1)、求数列 的通项公式;(2)、若数列 满足 ,且 .求数列 的通项公式,并求其前 项和 .18. 某大学导师计划从自己所培养的研究生甲、乙两人中选一人,参加雄安新区某部门组织的计算机技能大赛,两人以往5次的比赛成绩统计如下:(满分100分,单位:分).
第一次
第二次
第三次
第四次
第五次
甲的成绩
87
87
84
100
92
乙的成绩
100
80
85
95
90
(1)、试比较甲、乙二人谁的成绩更稳定;
(2)、在一次考试中若两人成绩之差的绝对值不大于2,则称两人“实力相当”.若从上述5次成绩中任意抽取2次,求恰有一次两人“实力相当”的概率.19. 如图,四棱台 中, 底面 ,平面 平面 为 的中点.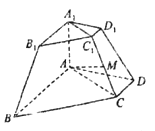 (1)、证明: ;
(1)、证明: ;
(2)、若 ,且 ,求点 到平面 的距离.20. 椭圆 的离心率为 ,且过点 .(1)、求椭圆 的方程;(2)、设 为椭圆 上任一点, 为其右焦点,点 满足 .①证明: 为定值;
②设直线 与椭圆 有两个不同的交点 ,与 轴交于点 .若 成等差数列,求 的值.