河北省唐山市乐亭县2016-2017学年七年级下学期数学期末考试试卷

试卷更新日期：2018-05-08 类型：期末考试

进入出卷网下载

一、单选题

1. 计算a³⋅a²正确的是（）

A、a B、 $a^{5}$ C、 $a^{6}$ D、 $a^{9}$

查看试题解析
2. 某种细菌直径约为0.00000067mm，若将0.00000067mm用科学记数法表示为 $6.7 \times 10^{n}$ mm（n为负整数），则n的值为（）.

A、-5 B、-6 C、-7 D、-8

查看试题解析
3. 下列三条线段不能构成三角形的三边的是（）

A、3cm，4cm，5cm B、5cm，6cm，11cm C、5cm，6cm，10cm D、2cm，3cm，4cm

查看试题解析
4. 如图，直线a，b被直线c所截，若a∥b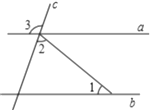， $∠ 1 = 40 ° ， ∠ 2 = 70 ° ，则 ∠ 3 =$ （）

A、70° B、100° C、110° D、120°

查看试题解析
5. 当x＜a＜0时，x²与ax的大小关系是（）

A、x²＞ax B、x²≥ax C、x²＜ax D、x²≤ax

查看试题解析
6. 不等式组 ${\begin{matrix} 4 x + 3 > 1 \\ 2 x- 8 \leq 16 - 4 x \end{matrix}$ 的最小整数解是（）.

A、0 B、-1 C、1 D、2

查看试题解析
7. 如图，下列能判定AB∥EF的条件有（）.
① $∠ B + ∠ B F E = 180 °$ ② $∠ 1 = ∠ 2$ ③ $∠ 3 = ∠ 4$ ④ $∠ B = ∠ 5$

A、1个 B、2个 C、3个 D、4个

查看试题解析
8. 当a，b互为相反数时，代数式 $a^{2}$ +ab-4的值为（）.

A、4 B、0 C、-3 D、-4

查看试题解析
9. 下列运算正确的是（）

A、（a+b）²=a²+b² B、（-2ab³）²=-4a²b⁶ C、3a²-2a³=a⁶ D、a³-a=a（a+1）（a-1）

查看试题解析
10. （-8） ²⁰¹⁴+（-8）²⁰¹³能被下列整数整除的是（）

A、3 B、5 C、7 D、9

查看试题解析
11. 若不等式组 ${\begin{matrix} 2 x - 1 < 3 \\ x < a \end{matrix}$ 的解集是x＜2，则a的取值范围是（）

A、a＜2 B、a≤2 C、a≥2 D、无法确定

查看试题解析
12. 如图，是三个等边三角形（注：等边三角形的三个内角都相等）随意摆放的图形，则 $∠ 1 + ∠ 2 + ∠ 3$ 等于（）

A、90° B、120° C、150° D、180°

查看试题解析
13.
把三张大小相同的正方形卡片A、B、C叠放在一个底面为正方形的盒底上，底面未被卡片覆盖的部分用阴影表示，若按图1摆放时，阴影部分的面积为S₁；若按图2摆放时，阴影部分的面积为S₂ ，则S₁与S₂的大小关系是（　　）

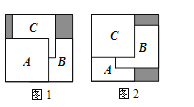A、S₁＞S₂ B、S₁＜S₂ C、S₁=S₂ D、无法确定

查看试题解析
14. 已知m²-m-1=0，则计算：m⁴-m³-m+2的结果为（）

A、3 B、-3 C、5 D、-5

查看试题解析
15. 甲、乙两人从相距24km的A、B两地沿着同一条公路相向而行，如果甲的速度是乙的速度的两倍，如果要保证在2小时以内相遇，则甲的速度（）

A、小于8km/h B、大于8km/h C、小于4km/h D、大于4km/h

查看试题解析
16. 如图，E是△ABC中BC边上的一点，且BE= $\frac{1}{3}$ BC；点D是AC上一点，且AD= $\frac{1}{4}$ AC， $S_{Δ A B C} = 24$ ，则 $S_{Δ B E F} - S_{Δ A D F} =$ （）

A、1 B、2 C、3 D、4

查看试题解析

二、填空题

17. 分解因式： $2 x^{2} - 2$ =

查看试题解析
18. 在△ABC中， $∠ A ： ∠ B ： ∠ C = 2 ： 3 ： 4 ，则 ∠ A$ 的度数为

查看试题解析
19. 已知不等式组 ${\begin{matrix} x + 1 < 2 a \\ x-b > 1 \end{matrix}$ 的解集是2＜x＜3，则关于x的方程ax+b=0的解为

查看试题解析
20. 如图，在△ABC中， $∠ A = 64 ° ， ∠ A B C 与 ∠ A C D$ 的平分线交于点 $A_{1}$ ， $得 ∠ A_{1}$ ， $∠ A_{1} B C$ 与 $∠ A_{1} C D$ 的平分线相交于点 $A_{2} ，得 ∠ A_{2} ： \dots ：$ $∠ A_{n- 1} B C 与 ∠ A_{n + 1} C D$ 的平分线交与点 $A_{n}$ ，要使∠An的度数为整数，则n的最大值为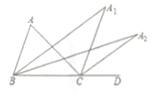

查看试题解析

三、解答题

21. 定义新运算为：对应任意实数a、b都有 $a \oplus b = （ a-b ） b- 1 ，$ 等式右边都是通常的加法、减法、乘法运算，比如 $1 \oplus 2$ =（1-2）×2-1=-3.

(1)、（-3） $\oplus$ 4的值为；

(2)、若x $\oplus$ 2的值小于5，求x的取值范围，并在如图所示的数轴上表示出来.

查看试题解析
22. 已知 $x^{2} - 5 x = 3$ ，求 $2 (x- 1) (2 x- 1) - 2 {(x + 1)}^{2} + 1$ 的值.

查看试题解析
23. 如图，AD∥BE，AE平分 $∠$ BAD，CD与AE相交于F， $∠$ CFE= $∠$ E。求证：AB∥CD.

查看试题解析
24. 如图，将一张矩形纸板按图中虚线裁剪成九块，其中有两块是边长都是m的大正方形，两块是边长都为n的小正方形，五块是长为m，宽为n的相同的小矩形，且m＞n.（以上长度单位：cm）

(1)、观察图形，可以发现代数式 $2 m^{2} + 5 mn + 2 n^{2}$ 可以因式分解为

(2)、若每块小矩形的面积为10cm $^{2}$ ，四个正方形的面积和为58cm $^{2}$ ，试求图中所有裁剪线（虚线部分）长之和.

查看试题解析
25. 如图（1），在△OBC中，点A是BO延长线上的一点，

(1)、 $∠ B = 32 ° ， ∠ C = 46 ° ，则 ∠ A O C =$ ，Q是BC边上一点，连结AQ交OC边于点P，如图（2），若 $∠ A = 18 ° ，则 ∠ O P Q$ =.
猜测： $∠ A + ∠ B + ∠ C 与 ∠ O P Q$ 的大小关系是；

(2)、将图（2）中的CO延长到点D，AQ延长到点E，连结DE，得到图（3），则 $∠ A Q B$ 等于图中哪三个角的和？并说明理由；

(3)、求图（3）中 $∠ A + ∠ D + ∠ B + ∠ E + ∠ C$ 的度数.

查看试题解析
26. 某商场销售A，B两种品牌的教学设备，这两种教学设备的进价和售价如下表所示：

A
B
进价（万元/套）
1.5
1.2
售价（万元/套）
1.65
1.4
该商场计划购进两种教学设备若干套，共需66万元，全部销售后可获毛利润9万元。
（毛利润=（售价-进价）×销售量）

(1)、该商场计划购进A，B两种品牌的教学设备各多少套？

(2)、通过市场调研，该商场决定在原计划的基础上，减少A种设备的购进数量，增加B种设备的购进数量，已知B种设备增加的数量是A种设备减少数量的1.5倍。若用于购进这两种教学设备的总资金不超过69万元，问A种设备购进数量至多减少多少套？

查看试题解析

	A	B
进价（万元/套）	1.5	1.2
售价（万元/套）	1.65	1.4