河北省承德市丰宁县2016-2017学年九年级上学期数学期末考试试卷
试卷更新日期:2018-05-08 类型:期末考试
一、单选题
-
1. sin30°=( )A、0 B、1 C、 D、2. 二次函数y=﹣2(x﹣1)2+3的图象的顶点坐标是( )A、(1,3) B、(﹣1,3) C、(1,﹣3) D、(﹣1,﹣3)3. 一元二次方程3x2﹣x=0的解是( )A、x=0 B、x1=0,x2=3 C、x1=0,x2= D、x=4. 如图,已知DE∥BC, ,则△ABC与△ADE的面积比为( )
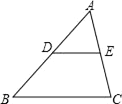 A、2:1 B、4:1 C、9:1 D、1:95. 半径为3的圆中,一条弦长为4,则圆心到这条弦的距离是( )A、3 B、4 C、 D、6. 已知:Rt△ABC中,∠C=90°,cosA= ,AB=15,则AC的长是( )A、3 B、6 C、9 D、127. 下列四个点中,在反比例函数y= 的图象上的是( )A、(3,-2) B、(3,2) C、(2,3) D、(-2,-3)8. 用配方法解方程x2+10x+9=0,配方正确的是( )A、(x+5)2=16 B、(x+5)2=34 C、(x﹣5)2=16 D、(x+5)2=259.
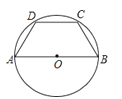
A、2:1 B、4:1 C、9:1 D、1:95. 半径为3的圆中,一条弦长为4,则圆心到这条弦的距离是( )A、3 B、4 C、 D、6. 已知:Rt△ABC中,∠C=90°,cosA= ,AB=15,则AC的长是( )A、3 B、6 C、9 D、127. 下列四个点中,在反比例函数y= 的图象上的是( )A、(3,-2) B、(3,2) C、(2,3) D、(-2,-3)8. 用配方法解方程x2+10x+9=0,配方正确的是( )A、(x+5)2=16 B、(x+5)2=34 C、(x﹣5)2=16 D、(x+5)2=259.如图,AB是圆O的直径,BC、CD、DA是圆O的弦,且BC=CD=DA,则∠BCD等于( )
 A、100° B、110° C、120° D、135°10.
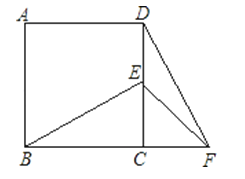
A、100° B、110° C、120° D、135°10.如图,在正方形ABCD中,E为DC边上的点,连接BE,将△BCE绕点C顺时针方向旋转90°得到△DCF,连接EF,若∠BEC=60°,则∠EFD的度数为( )
 A、10° B、15° C、20° D、25°11. 反比例函数y= 的图象如图所示,以下结论:
A、10° B、15° C、20° D、25°11. 反比例函数y= 的图象如图所示,以下结论:①常数m<﹣1;
②在每个象限内,y随x的增大而增大;
③若A(﹣1,h),B(2,k)在图象上,则h<k;
④若P(x,y)在图象上,则P′(﹣x,﹣y)也在图象上.
其中正确的是( )
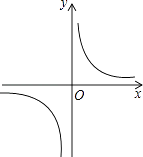 A、①② B、②③ C、③④ D、①④12. 如图,在Rt△ABC中,∠BAC=90°,AD⊥BC,若AB=2,BC=4.则DC的长度为( )
A、①② B、②③ C、③④ D、①④12. 如图,在Rt△ABC中,∠BAC=90°,AD⊥BC,若AB=2,BC=4.则DC的长度为( ) A、1 B、 C、3 D、213. 一小球被抛出后,距离地面的高度h(米)和飞行时间t(秒)满足下面函数关系式:h=-5(t-1)2+6,则小球距离地面的最大高度是( )
A、1 B、 C、3 D、213. 一小球被抛出后,距离地面的高度h(米)和飞行时间t(秒)满足下面函数关系式:h=-5(t-1)2+6,则小球距离地面的最大高度是( )
A、1米 B、5米 C、6米 D、7米14. 二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论正确的是( )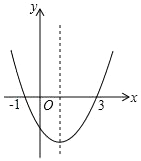 A、a<0 B、c>0 C、a+b+c>0 D、方程 ax2+bx+c=0的两根是x1=﹣1,x2=315. 图中,EB为半圆O的直径,点A在EB的延长线上,AD切半圆O于点D,BC⊥AD于点C,AB=2,半圆O的半径为2,则BC的长为( )
A、a<0 B、c>0 C、a+b+c>0 D、方程 ax2+bx+c=0的两根是x1=﹣1,x2=315. 图中,EB为半圆O的直径,点A在EB的延长线上,AD切半圆O于点D,BC⊥AD于点C,AB=2,半圆O的半径为2,则BC的长为( )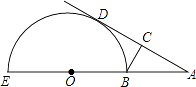 A、2 B、1 C、1.5 D、0.516. 如图,在直角梯形ABCD中,AD∥BC,∠ABC=90°,AB=12,AD=4,BC=9,点P是AB上一动点.若△PAD与△PBC是相似三角形,则满足条件的点P的个数有( )
A、2 B、1 C、1.5 D、0.516. 如图,在直角梯形ABCD中,AD∥BC,∠ABC=90°,AB=12,AD=4,BC=9,点P是AB上一动点.若△PAD与△PBC是相似三角形,则满足条件的点P的个数有( )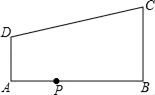 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
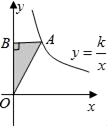
17. 点P(﹣3,4)关于原点对称的点的坐标为18. 如图,已知A点是反比例函数 (k≠0)的图象上一点,AB⊥y轴于B,且△ABO的面积为3,则k的值为
 19. 如图,将长为8cm的铁丝首尾相接围成半径为2cm的扇形.则S扇形=cm2 .
19. 如图,将长为8cm的铁丝首尾相接围成半径为2cm的扇形.则S扇形=cm2 .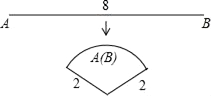 20. 在平行四边形ABCD中,E为CD的中点,△DOE的面积是2,△DOA的面积
20. 在平行四边形ABCD中,E为CD的中点,△DOE的面积是2,△DOA的面积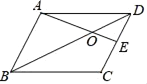
三、解答题
-
21. 如图,△OAB中,OA=OB=10cm,∠AOB=80°,以点O为圆心,半径为6cm的优弧弧MN分别交OA,OB于点M,N.
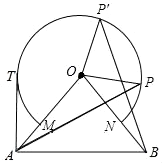 (1)、点P在右半弧上(∠BOP是锐角),将OP绕点O逆时针旋转80°得OP′.求证:AP=BP′;(2)、点T在左半弧上,若AT与弧相切,求AT的长.22. 如图,抛物线y=ax2+bx﹣4a经过A(﹣1,0)、C(0,4)两点,与x轴交于另一点B.
(1)、点P在右半弧上(∠BOP是锐角),将OP绕点O逆时针旋转80°得OP′.求证:AP=BP′;(2)、点T在左半弧上,若AT与弧相切,求AT的长.22. 如图,抛物线y=ax2+bx﹣4a经过A(﹣1,0)、C(0,4)两点,与x轴交于另一点B.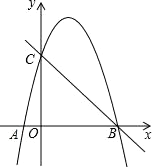 (1)、求抛物线的解析式;(2)、求抛物线的顶点坐标(3)、已知点D(m,m+1)在第一象限的抛物线上,求点D的坐标.23. 如图,在一笔直的海岸线l上有AB两个观测站,A在B的正东方向,AB=2(单位:km).有一艘小船在点P处,从A测得小船在北偏西60°的方向,从B测得小船在北偏东45°的方向.(结果都保留根号)
(1)、求抛物线的解析式;(2)、求抛物线的顶点坐标(3)、已知点D(m,m+1)在第一象限的抛物线上,求点D的坐标.23. 如图,在一笔直的海岸线l上有AB两个观测站,A在B的正东方向,AB=2(单位:km).有一艘小船在点P处,从A测得小船在北偏西60°的方向,从B测得小船在北偏东45°的方向.(结果都保留根号)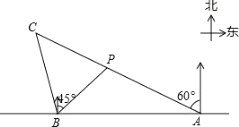 (1)、求点P到海岸线l的距离;(2)、小船从点P处沿射线AP的方向航行一段时间后,到点C处,此时,从B测得小船在北偏西15°的方向.求点C与点B之间的距离.24. 某水果专卖店销售樱桃,其进价为每千克40元,按每千克60元出售,平均每天可售出100千克,后来经过市场调查发现,单价每千克降低1元,则平均每天的销售可增加10千克,请回答:(1)、写出售价为50元时,每天能卖樱桃千克,每天获得利润元.(2)、若该专卖店销售这种樱桃要想平均每天获利2240元,每千克樱桃应降价多少元?(3)、若该专卖店销售这种樱桃要想平均每天获利最大,每千克樱桃应售价多少元?25. 阅读理解:如图①,在四边形ABCD的边AB上任取一点E(点E不与A、B重合),分别连接ED、EC,可以把四边形ABCD分成三个三角形,如果其中有两个三角形相似,我们就把E叫做四边形ABCD的边AB上的“相似点”;如果这三个三角形都相似,我们就把E叫做四边形ABCD的边AB上的“强相似点”.解决问题:
(1)、求点P到海岸线l的距离;(2)、小船从点P处沿射线AP的方向航行一段时间后,到点C处,此时,从B测得小船在北偏西15°的方向.求点C与点B之间的距离.24. 某水果专卖店销售樱桃,其进价为每千克40元,按每千克60元出售,平均每天可售出100千克,后来经过市场调查发现,单价每千克降低1元,则平均每天的销售可增加10千克,请回答:(1)、写出售价为50元时,每天能卖樱桃千克,每天获得利润元.(2)、若该专卖店销售这种樱桃要想平均每天获利2240元,每千克樱桃应降价多少元?(3)、若该专卖店销售这种樱桃要想平均每天获利最大,每千克樱桃应售价多少元?25. 阅读理解:如图①,在四边形ABCD的边AB上任取一点E(点E不与A、B重合),分别连接ED、EC,可以把四边形ABCD分成三个三角形,如果其中有两个三角形相似,我们就把E叫做四边形ABCD的边AB上的“相似点”;如果这三个三角形都相似,我们就把E叫做四边形ABCD的边AB上的“强相似点”.解决问题: (1)、如图①,∠A=∠B=∠DEC=45°,试判断点E是否是四边形ABCD的边AB上的相似点,并说明理由;(2)、如图②,在矩形ABCD中,A、B、C、D四点均在正方形网格(网格中每个小正方形的边长为1)的格点(即每个小正方形的顶点)上,试在图②中画出矩形ABCD的边AB上的强相似点;(3)、如图③,将矩形ABCD沿CM折叠,使点D落在AB边上的点E处,若点E恰好是四边形ABCM的边AB上的一个强相似点,试探究AB与BC的数量关系.
(1)、如图①,∠A=∠B=∠DEC=45°,试判断点E是否是四边形ABCD的边AB上的相似点,并说明理由;(2)、如图②,在矩形ABCD中,A、B、C、D四点均在正方形网格(网格中每个小正方形的边长为1)的格点(即每个小正方形的顶点)上,试在图②中画出矩形ABCD的边AB上的强相似点;(3)、如图③,将矩形ABCD沿CM折叠,使点D落在AB边上的点E处,若点E恰好是四边形ABCM的边AB上的一个强相似点,试探究AB与BC的数量关系.