2018年高考数学提分专练：第20题平面解析几何（解答题）

试卷更新日期：2018-05-08 类型：二轮复习

进入出卷网下载

一、真题演练

1. 设A，B为曲线C：y= $\frac{x^{2}}{4}$ 上两点，A与B的横坐标之和为4．

(1)、求直线AB的斜率；

(2)、设M为曲线C上一点，C在M处的切线与直线AB平行，且AM⊥BM，求直线AB的方程．

查看试题解析
2. 已知椭圆C： $\frac{x^{2}}{a^{2}}$ + $\frac{y^{2}}{b^{2}}$ =1（a＞b＞0），四点P₁（1，1），P₂（0，1），P₃（﹣1， $\frac{\sqrt{3}}{2}$ ），P₄（1， $\frac{\sqrt{3}}{2}$ ）中恰有三点在椭圆C上．

(1)、求C的方程；

(2)、设直线l不经过P₂点且与C相交于A，B两点．若直线P₂A与直线P₂B的斜率的和为﹣1，证明：l过定点．

查看试题解析
3. 设O为坐标原点，动点M在椭圆C： $\frac{x^{2}}{2}$ +y²=1上，过M做x轴的垂线，垂足为N，点P满足 $\vec{N P}$ = $\sqrt{2} \vec{N M}$ ．
（Ⅰ）求点P的轨迹方程；
（Ⅱ）设点Q在直线x=﹣3上，且 $\vec{O P}$ • $\vec{P Q}$ =1．证明：过点P且垂直于OQ的直线l过C的左焦点F．

查看试题解析
4. 在直角坐标系xOy中，曲线y=x²+mx﹣2与x轴交于A、B两点，点C的坐标为（0，1），当m变化时，解答下列问题：

(1)、能否出现AC⊥BC的情况？说明理由；

(2)、证明过A、B、C三点的圆在y轴上截得的弦长为定值．

查看试题解析
5. 已知抛物线C：y²=2x，过点（2，0）的直线l交C与A，B两点，圆M是以线段AB为直径的圆．
（Ⅰ）证明：坐标原点O在圆M上；
（Ⅱ）设圆M过点P（4，﹣2），求直线l与圆M的方程．

查看试题解析

二、模拟实训

6. 已知椭圆 $C : \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 上动点 $P$ 到两焦点 $F_{1}, F_{2}$ 的距离之和为4，当点 $P$ 运动到椭圆 $C$ 的一个顶点时，直线 $P F_{1}$ 恰与以原点 $O$ 为圆心，以椭圆 $C$ 的离心率 $e$ 为半径的圆相切.

(1)、求椭圆 $C$ 的方程；

(2)、设椭圆 $C$ 的左右顶点分别为 $A 、 B$ ，若 $P A 、 P B$ 交直线 $x = 6$ 于 $M 、 N$ 两点.问以 $M N$ 为直径的圆是否过定点？若是，请求出该定点坐标；若不是，请说明理由.

查看试题解析
7. 已知椭圆 $C_{1} : \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 的离心率为 $\frac{\sqrt{2}}{2}, P (- 2, 0)$ 是它的一个顶点，过点 $P$ 作圆 $C_{2} : x^{2} + y^{2} = r^{2}$ 的切线 $P T, T$ 为切点，且 $| P T | = \sqrt{2}$ .

(1)、求椭圆 $C_{1}$ 及圆 $C_{2}$ 的方程；

(2)、过点 $P$ 作互相垂直的两条直线 $l_{1}, l_{2}$ ，其中 $l_{1}$ 与椭圆的另一交点为 $D$ ， $l_{2}$ 与圆交于 $A, B$ 两点，求 $△ A B D$ 面积的最大值.

查看试题解析
8. 如图，在平面直角坐标系xOy中，过椭圆C： $\frac{x^{2}}{4} + y^{2} = 1$ 的左顶点A作直线l，与椭圆C和y轴正半轴分别交于点P，Q．

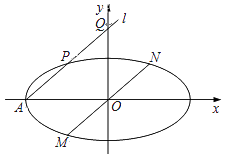(1)、若AP=PQ，求直线l的斜率；

(2)、过原点O作直线l的平行线，与椭圆C交于点M，N，求证： $\frac{A P \cdot A Q}{M N^{2}}$ 为定值．

查看试题解析
9.
如图，已知椭圆 $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$ （a＞b＞0）的左右顶点分别是A（﹣ $\sqrt{2}$ ，0），B（ $\sqrt{2}$ ，0），离心率为 $\frac{\sqrt{2}}{2}$ ．设点P（a，t）（t≠0），连接PA交椭圆于点C，坐标原点是O．

（Ⅰ）证明：OP⊥BC；
（Ⅱ）若三角形ABC的面积不大于四边形OBPC的面积，求|t|的最小值．

查看试题解析
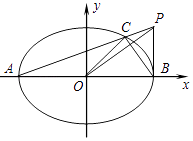10.
如图，在矩形ABCD中，|AB|=4，|AD|=2，O为AB中点，P，Q分别是AD和CD上的点，且满足① $\frac{| A P |}{| A D |}$ = $\frac{| D Q |}{| D C |}$ ，②直线AQ与BP的交点在椭圆E： $\frac{x^{2}}{a^{2}}$ + $\frac{y^{2}}{b^{2}}$ =1（a＞b＞0）上．

（Ⅰ）求椭圆E的方程；
（Ⅱ）设R为椭圆E的右顶点，M为椭圆E第一象限部分上一点，作MN垂直于y轴，垂足为N，求梯形ORMN面积的最大值．

查看试题解析
11. 已知椭圆 $C : \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 的离心率为 $\frac{\sqrt{3}}{2}$ ，且过点 $A (2, 1)$ ．
（Ⅰ）求椭圆 $C$ 的方程．
（Ⅱ）若 $P$ ， $Q$ 是椭圆 $C$ 上两个不同的动点，且使 $∠ P A Q$ 的角平分线垂直于 $x$ 轴，试判断直线 $P Q$ 的斜率是否为定值？若是，求出该值；若不是，说明理由．

查看试题解析
12. 在平面直角坐标系 $x O y$ 中，点 $F_{1} (- \sqrt{3}, 0)$ ，圆 $F_{2} : x^{2} + y^{2} - 2 \sqrt{3} x - 13 = 0$ ，以动点P为圆心的圆经过点 $F_{1}$ ，且圆P与圆 $F_{2}$ 内切.
（Ⅰ）求动点P的轨迹E的方程；
（Ⅱ）若直线l过点 $(1, 0)$ ，且与曲线E交于 $A, B$ 两点，则在x轴上是否存在一点 $D (t, 0) (t \neq 0)$ ，使得x轴平分 $∠ A D B$ ？若存在，求出t的值；若不存在，请说明理由.

查看试题解析
13. 已知点E（﹣2，0），点P时圆F：（x﹣2）²+y²=36上任意一点，线段EP的垂直平分线交FP于点M，点M的轨迹记为曲线C．
（Ⅰ）求曲线C的方程；
（Ⅱ）过F的直线交曲线C于不同的A、B两点，交y轴于点N，已知 $\vec{N A}$ =m $\vec{A F}$ ， $\vec{N B}$ =n $\vec{B F}$ ，求m+n的值．

查看试题解析
14.
已知直线l的方程为y=x+2，点P是抛物线y²=4x上到直线l距离最小的点，点A是抛物线上异于点P的点，直线AP与直线l交于点Q，过点Q与x轴平行的直线与抛物线y²=4x交于点B．

（Ⅰ）求点P的坐标；
（Ⅱ）证明直线AB恒过定点，并求这个定点的坐标．

查看试题解析
15. 已知椭圆C： $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}}$ =1（a＞b＞0）的左、右顶点分别为A₁、A₂ ，上、下顶点分别为B₂、B₁ ， O为坐标原点，四边形A₁B₁A₂B₂的面积为4，且该四边形内切圆的方程为x²+y²= $\frac{4}{5}$ ．

（Ⅰ）求椭圆C的方程；
（Ⅱ）若M、N是椭圆C上的两个不同的动点，直线OM、ON的斜率之积等于﹣ $\frac{1}{4}$ ，试探求△OMN的面积是否为定值，并说明理由．

查看试题解析

2018年高考数学提分专练：第20题 平面解析几何（解答题）

一、真题演练

二、模拟实训

2018年高考数学提分专练：第20题平面解析几何（解答题）