河南省2018届普通高中毕业班4月文数高考适应性考试试卷
试卷更新日期:2018-05-08 类型:高考模拟
一、选择题
-
1. 已知集合 , ,则 ( )
A、 B、 C、 D、2. 若复数 ( 是虚数单位),则 ( )
A、 B、 C、 D、3. 下列说法中,正确的是( )
A、命题“若 ,则 ”的逆命题是真命题 B、命题“ , ”的否定是“ , ” C、命题“ 或 ”为真命题,则命题“ ”和命题“ ”均为真命题 D、已知 ,则“ ”是“ ”的充分不必要条件4. 在一组样本数据 , ,…, ( , , ,…, 不全相等)的散点图中,若所有样本点 都在直线 上,则这组样本数据的样本相关系数为( )
A、-3 B、0 C、-1 D、15. 已知函数 在点 处的切线为 ,动点 在直线 上,则 的最小值是( )A、4 B、2 C、 D、6. 执行如图所示的程序框图,则输出 的值为( )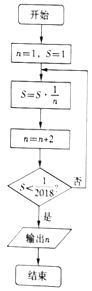 A、14 B、13 C、12 D、117. 函数 的图像与函数 的图像( )
A、14 B、13 C、12 D、117. 函数 的图像与函数 的图像( )
A、有相同的对称轴但无相同的对称中心 B、有相同的对称中心但无相同的对称轴 C、既有相同的对称轴也有相同的对称中心 D、既无相同的对称中心也无相同的对称轴8. 三国时期我国的数学家赵爽曾创制了一幅“勾股圆方图”,用数形结合的方法给出了勾股定理的详细证明.如图所示的“勾股圆方图”中,四个相同的直角三角形与中间的小正方形拼成一个大正方形,其中直角三角形中较小的锐角 满足 ,现在向该正方形区域内随机投掷一枚飞镖,则飞镖落在小正方形内的概率是( )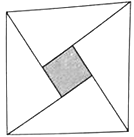 A、 B、 C、 D、9. 已知四棱锥 的三视图如图所示,则四棱锥 的五个面中面积的最大值是( )
A、 B、 C、 D、9. 已知四棱锥 的三视图如图所示,则四棱锥 的五个面中面积的最大值是( )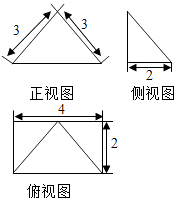 A、3 B、6 C、8 D、1010. 设 , 是双曲线 : 的两个焦点, 是 上一点,若 ,且 的最小内角的大小为 ,则双曲线 的渐近线方程是( )
A、3 B、6 C、8 D、1010. 设 , 是双曲线 : 的两个焦点, 是 上一点,若 ,且 的最小内角的大小为 ,则双曲线 的渐近线方程是( )
A、 B、 C、 D、11. 已知等差数列 的前 项和为 ,且 ,若数列 为递增数列,则实数 的取值范围为( )
A、 B、 C、 D、12. 定义域为 的函数 的图象的两个端点分别为 , , 是 图象上任意一点,其中 ,向量 .若不等式 恒成立,则称函数 在 上为“ 函数”.若函数 在 上为“ 函数”,则实数 的取值范围是( )
A、 B、 C、 D、二、填空题
-
13. 已知实数 , 满足不等式组 ,则 的最小值为
14. 已知点 , ,向量 ,则
15. 已知点 是抛物线 的焦点, , 是该抛物线上两点, ,则线段 的中点的横坐标为
16. 设函数 的定义域为 ,若对于任意 ,当 时,恒有 ,则称点 为函数 图象的对称中心.研究函数 的某一个对称中心,并利用对称中心的上述定义,可得到 的值为
三、解答题
-
17. 的内角 , , 的对边分别为 , , ,面积为 ,已知 .
(1)、求角 ;(2)、若 , ,求角 .18. 如图,在四棱锥 中,底面 是正方形, 底面 , , 分别是 , 的中点,且 .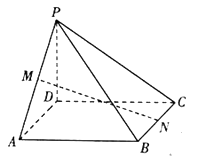 (1)、求证: 平面 ;(2)、求点 到平面 的距离.19. 进入12月以来,某地区为了防止出现重污染天气,坚持保民生、保蓝天,严格落实机动车限行等一系列“管控令”.该地区交通管理部门为了了解市民对“单双号限行”的赞同情况,随机采访了220名市民,将他们的意见和是否拥有私家车情况进行了统计,得到如下的 列联表:
(1)、求证: 平面 ;(2)、求点 到平面 的距离.19. 进入12月以来,某地区为了防止出现重污染天气,坚持保民生、保蓝天,严格落实机动车限行等一系列“管控令”.该地区交通管理部门为了了解市民对“单双号限行”的赞同情况,随机采访了220名市民,将他们的意见和是否拥有私家车情况进行了统计,得到如下的 列联表:赞同限行
不赞同限行
合计
没有私家车
90
20
110
有私家车
70
40
110
合计
160
60
220
附: .
0.10
0.05
0.025
0.010
0.005
0.001
2.706
3.841
5.024
6.635
7.879
10.828
(1)、根据上面的列联表判断,能否在犯错误的概率不超过0.001的前提下认为“是否赞同限行与是否拥有私家车”有关;(2)、为了了解限行之后是否对交通拥堵、环境污染起到改善作用,从上述调查的不赞同限行的人员中按分层抽样抽取6人,再从这6人中随机抽出3名进行电话回访,求3人中至少抽到1名“没有私家车”人员的概率.20. 在平面直角坐标系 中,已知椭圆 : 的离心率 , , 分别为左、右焦点,过 的直线交椭圆 于 , 两点,且 的周长为8.(1)、求椭圆 的方程;(2)、设过点 的直线交椭圆 于不同两点 , . 为椭圆上一点,且满足 ( 为坐标原点),当 时,求实数 的取值范围.