海南省2018届高三理数第二次联合考试试卷
试卷更新日期:2018-05-08 类型:高考模拟
一、选择题
-
1. 设集合 , ,则 ( )
A、 B、 C、 D、2. 已知复数 在复平面内对应的点在第二象限,则整数 的取值为( )
A、0 B、1 C、2 D、33. 设向量 , ,若向量 与 同向,则 ( )
A、 B、 C、 D、4. 等差数列 的前 项和为 , ,且 ,则 的公差 ( )
A、1 B、2 C、3 D、45. 某几何体的三视图如图所示,其中圆的半径均为1,则该几何体的体积为( )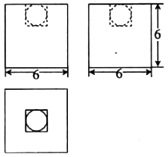 A、 B、 C、 D、6. 设 , 满足约束条件 ,则 的最小值是( )
A、 B、 C、 D、6. 设 , 满足约束条件 ,则 的最小值是( )
A、0 B、-1 C、-2 D、-37. 我国古代数学名著《算法统宗》中有如下问题:“远望巍巍塔七层,红光点点倍加增,共灯三百八十一,请问尖头几盏灯?”意思是:“一座7层塔共挂了381盏灯,且相邻两层中的下一层灯数是上一层灯数的2倍,则塔的顶层共有灯多少?”现有类似问题:一座5层塔共挂了242盏灯,且相邻两层中的下一层灯数是上一层灯数的3倍,则塔的底层共有灯( )
A、81盏 B、112盏 C、114盏 D、162盏8. 执行如图所示的程序框图,则输出的 ( )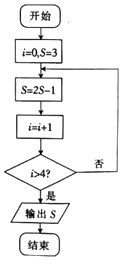 A、17 B、33 C、65 D、1299. 将曲线 向右平移 个单位长度后得到曲线 ,若函数 的图象关于 轴对称,则 ( )
A、17 B、33 C、65 D、1299. 将曲线 向右平移 个单位长度后得到曲线 ,若函数 的图象关于 轴对称,则 ( )
A、 B、 C、 D、10. 在平面直角坐标系 中,双曲线 : 的一条渐近线与圆 相切,则 的离心率为( )
A、 B、 C、 D、11. 在侦破某一起案件时,警方要从甲、乙、丙、丁四名可疑人员中查出真正的嫌疑人,现有四条明确信息:(1)此案是两人共同作案;(2)若甲参与此案,则丙一定没参与;(3)若乙参与此案,则丁一定参与;(4)若丙没参与此案,则丁也一定没参与.据此可以判断参与此案的两名嫌疑人是( )
A、甲、乙 B、乙、丙 C、甲、丁 D、丙、丁12. 在四面体 中, 底面 , , , 为棱 的中点,点 在 上且满足 ,若四面体 的外接球的表面积为 ,则 ( )
A、 B、2 C、 D、二、填空题
-
13. 若 是函数 的一个极值点,则实数
14. 如图,小林从位于街道 处的家里出发,先到 处的二表哥家拜年,再和二表哥一起到位于 处的大表哥家拜年,则小林到大表哥家可以选择的最短路径的条数为 15. 某超市经营的某种包装优质东北大米的质量 (单位: )服从正态分布 ,任意选取一袋这种大米,质量在 的概率为(附:若 ,则 , , )
15. 某超市经营的某种包装优质东北大米的质量 (单位: )服从正态分布 ,任意选取一袋这种大米,质量在 的概率为(附:若 ,则 , , )
16. 已知 F 是抛物线 C : 的焦点, P 是 C 上一点,直线 FP 交直线 y=-3 于点 Q .若 ,则 |PQ| .
三、解答题
-
17. 的内角 , , 所对的边分别为 , , .已知 ,且 .
(1)、求角 ;(2)、若 ,且 的面积为 ,求 的周长.18. 从某小区抽取50户居民进行月用电量调查,发现其用电量都在50到350度之间,频率分布直方图如下.
附表及公式:
0.050
0.010
0.001
3.841
6.635
10.828
, .
(1)、求频率分布直方图中 的值并估计这50户用户的平均用电量;(2)、若将用电量在区间 内的用户记为 类用户,标记为低用电家庭,用电量在区间 内的用户记为 类用户,标记为高用电家庭,现对这两类用户进行问卷调查,让其对供电服务进行打分,打分情况见茎叶图: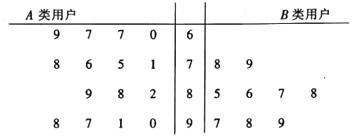
①从 类用户中任意抽取1户,求其打分超过85分的概率;
②若打分超过85分视为满意,没超过85分视为不满意,请填写下面列联表,并根据列联表判断是否有 的把握认为“满意度与用电量高低有关”?
满意
不满意
合计
类用户
类用户
合计
19. 如图,在四棱锥 中,底面 为平行四边形, , ,且 底面 .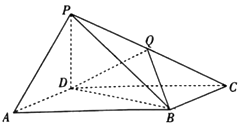 (1)、证明:平面 平面 ;(2)、若 为 的中点,且 ,求二面角 的大小.
(1)、证明:平面 平面 ;(2)、若 为 的中点,且 ,求二面角 的大小.
20. 在平面直角坐标系 中,设动点 到坐标原点的距离与到 轴的距离分别为 , ,且 ,记动点 的轨迹为 .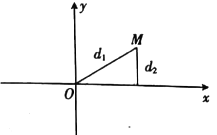 (1)、求 的方程;(2)、设过点 的直线 与 相交于 , 两点,当 的面积最大时,求 .
(1)、求 的方程;(2)、设过点 的直线 与 相交于 , 两点,当 的面积最大时,求 .