北京市门头沟区2016-2017学年七年级下学期数学期末考试试卷

试卷更新日期：2018-05-08 类型：期末考试

进入出卷网下载

一、单选题

1. 点P（2，1）在平面直角坐标系中所在的象限是（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
2. 计算 $5^{0}$ 的结果是（）

A、0 B、1 C、50 D、5

查看试题解析
3. 人体中成熟的红细胞平均直径为0.00077厘米，将数字0.00077用科学记数法表示为（）

A、 $7.7 \times 10^{- 3}$ B、 $77 \times 10^{- 4}$ C、 $77 \times 10^{- 3}$ D、 $7.7 \times 10^{- 4}$

查看试题解析
4. 下列计算正确的是（）

A、 $a^{3} \cdot a^{3} = 2 a^{6}$ B、 $a^{3} + a^{3} = a^{6}$ C、 $a^{3} \div a^{5} = \frac{1}{a^{2}}$ D、 ${(a^{3})}^{3} = a^{6}$

查看试题解析
5. 已知 $a < b$ ，下列变形正确的是（）

A、 $a - 3 > b - 3$ B、 $3 a - 1 > 3 b - 1$ C、 $- 3 a > - 3 b$ D、 $\frac{a}{3} > \frac{b}{3}$

查看试题解析
6. 如图，将三角板的直角顶点放在直尺的一边上，如果∠1=65°，那么∠2的度数为（）

A、10° B、15° C、20° D、25°

查看试题解析
7. 在下列命题中，为真命题的是（）

A、相等的角是对顶角 B、平行于同一条直线的两条直线互相平行 C、同旁内角互补 D、垂直于同一条直线的两条直线互相垂直

查看试题解析
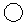8. 如图，在一个三角形三个顶点和中心处的每个“ ”中各填有一个式子，如果图中任意三个“ 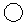”中的式子之和均相等，那么a的值为（）

A、1 B、2 C、3 D、0

查看试题解析
9. 右图是某市 10 月 1 日至10 月 7 日一周内的“日平均气温变化统计图”．在“日平均气温”这组数据中，众数和中位数分别是（）

A、13，13 B、14，14 C、13，14 D、14，13

查看试题解析
10. 如图，在平面直角坐标系xOy中，点P（1，0）．点P第1次向上跳动1个单位至点P₁（1，1），紧接着第2次向左跳动2个单位至点P₂（－1，1），第3次向上跳动1个单位至点P₃ ，第4次向右跳动3个单位至点P₄ ，第5次又向上跳动1个单位至点P₅ ，第6次向左跳动4个单位至点P₆ ， ……．照此规律，点P第100次跳动至点P₁₀₀的坐标是（）

A、（－26，50） B、（－25，50） C、（26，50） D、（25，50）

查看试题解析

二、填空题

11. 如果把方程 $3 x + y = 2$ 写成用含x的代数式表示y的形式，那么y =.

查看试题解析
12. 右图中四边形均为长方形，根据图形，写出一个正确的等式：

查看试题解析
13. 因式分解： $a^{3} - 4 a =$

查看试题解析
14. 如果∠1与∠2互余，∠3与∠2互余，∠1=35°，那么∠3 =度．

查看试题解析
15. 如果关于x ， y二元一次方程组 ${\begin{matrix} 3 x + y = 1 + a ， \\ x + 3 y = 3 \end{matrix}$ 的解满足 $x + y < 2$ ，那么a的取值范围是

查看试题解析
16. 《九章算术》是中国传统数学最重要的著作，奠定了中国传统数学的基本框架．它的代数成就主要包括开方术、正负术和方程术．其中，方程术是《九章算术》最高的数学成就．《九章算术》中记载：“今有牛五、羊二，直金十两；牛二、羊五，直金八两．问：牛、羊各直金几何？”译文：“假设有5头牛、2只羊，值金10两；2 头牛、5只羊，值金8两．问：每头牛、每只羊各值金多少两？”设每头牛值金x两，每只羊值金y 两，可列方程组为

查看试题解析
17. 如图，直线AB、CD、EF相交于点O ， AB⊥CD ， OG平分∠AOE ，如果∠FOD = 28°，那么∠AOG =度．

查看试题解析
18. 学完一元一次不等式解法后，老师布置了如下练习：
解不等式 $\frac{15 - 3 x}{2}$ ≥ $7 - x$ ，并把它的解集在数轴上表示出来．
以下是小明的解答过程：
问：请指出小明从第几步开始出现了错误，并说明判断依据．
答：

查看试题解析

三、解答题

19. 计算：

(1)、 ${(a - 1)}^{2} - a (a - 2)$ ；

(2)、 $(x - 6) (x + 4) + (3 x + 2) (2 - 3 x)$ ．

查看试题解析
20. 解下列方程组：

(1)、 ${\begin{matrix} y = 5 - x ， \\ x - 2 y = 2 ； \end{matrix}$ ；

(2)、 ${\begin{matrix} 2 x - 3 y = 3 \\ 3 x - 2 y = 7 \end{matrix}$

查看试题解析
21. 已知 $x = \frac{1}{2}$ ， $y = \frac{1}{3}$ ，求 ${(x + y)}^{2} + (x + y) (x - y) - 2 x^{3} y \div x y$ 的值．

查看试题解析
22. 解不等式组 ${\begin{matrix} 4 (x + 1) \leq 7 x + 10 \\ x - 5 < \frac{x - 8}{3} \end{matrix}$ 并写出它的所有非负整数解．

查看试题解析
23. 完成下面的证明：
已知：如图，D是BC上任意一点，BE⊥AD ，交AD的延长线于点E ， CF⊥AD ，垂足为F ．
求证：∠1＝∠2．
证明：∵ BE⊥AD（已知），
∴ ∠BED＝°（）．
又∵ CF⊥AD（已知），
∴ ∠CFD＝°．
∴ ∠BED＝∠CFD（等量代换）．
∴ BE∥CF（）．
∴ ∠1＝∠2（）．

查看试题解析
24. 为了更好的开展“我爱阅读”活动，小明针对某校七年级学生（共16个班，480名学生）课外阅读喜欢图书的种类（每人只能选一种书籍）进行了调查．

(1)、小明采取的下列调查方式中，比较合理的是；理由是：．
A．对七年级（1）班的全体同学进行问卷调查；
B．对七年级各班的语文科代表进行问卷调查；
C．对七年级各班学号为3的倍数的全体同学进行问卷调查．

(2)、小明根据问卷调查的结果绘制了如下两幅不完整的统计图，根据图中提供的信息解答下列问题：
①在扇形统计图中，“其它”所在的扇形的圆心角等于多少度；
②补全条形统计图；
③根据调查结果，估计七年级课外阅读喜欢“漫画”的同学有多少人．

查看试题解析
25. 为建设京西绿色走廊，改善永定河水质，某治污公司决定购买10台污水处理设备．现有A、B两种型号的设备，其中每台的价格与月处理污水量如下表：
经调查：购买一台A型设备比购买一台B型设备多2万元，购买2台A型设备比购买3台B型设备少6万元．

(1)、求x、y的值；

(2)、如果治污公司购买污水处理设备的资金不超过105万元，求该治污公司有哪几种购买方案；

(3)、在（2）的条件下，如果月处理污水量不低于2040吨，为了节约资金，请为该公司设计一种最省钱的购买方案．

查看试题解析
26. 已知：△ABC和同一平面内的点D ．

(1)、如图1，点D在BC边上，过D作DE∥BA交AC于E ， DF∥CA交AB于F ．
① 依题意，在图1中补全图形；
② 判断∠EDF与∠A的数量关系，并直接写出结论（不需证明）．

(2)、如图2，点D在BC的延长线上，DF∥CA ， ∠EDF=∠A ．判断DE与BA的位置关系，并证明．

(3)、如图3，点D是△ABC外部的一个动点，过D作DE∥BA交直线AC于E ， DF∥CA交直线AB于F ，直接写出∠EDF与∠A的数量关系（不需证明）．

查看试题解析
27. 定义一种新运算“ $a ☆ b$ ”的含义为：
当 $a \geq b$ 时， $a ☆ b = a + b$ ；当 $a < b$ 时， $a ☆ b = a - b$ ．
例如： $3 ☆ (- 4) = 3 + (- 4) = - 1$ ， $(- 6) ☆ \frac{1}{2} = (- 6) - \frac{1}{2} = - 6 \frac{1}{2}$ ．

(1)、填空： $(- 4) ☆ 3 =$ ；

(2)、如果 $(3 x - 4) ☆ (2 x + 8) = (3 x - 4) - (2 x + 8)$ ，求x的取值范围；

(3)、填空： $(x^{2} - 2 x + 3) ☆ (- x^{2} + 2 x - 5) =$ ；

(4)、如果 $(3 x - 7) ☆ (3 - 2 x) = 2$ ，求x的值．

查看试题解析