上海市杨浦区2018届高三下学期数学质量调研二模试卷
试卷更新日期:2018-05-08 类型:高考模拟
一、单选题
-
1. 已知函数 的图象如图所示,则 的值为( )
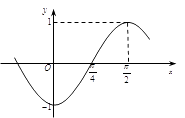 A、 B、 C、 D、2. 设A、B是非空集合,定义: 且 .已知 , ,则 等于( )A、 B、 C、 D、3. 已知 , ,则“ ”是“直线 与 平行”的( )条件
A、 B、 C、 D、2. 设A、B是非空集合,定义: 且 .已知 , ,则 等于( )A、 B、 C、 D、3. 已知 , ,则“ ”是“直线 与 平行”的( )条件
A、充分非必要 B、必要非充分 C、充要 D、既非充分也非必要4. 已知长方体的表面积为 ,棱长的总和为24. 则长方体的体对角线与棱所成角的最大值为( )
A、 B、 C、 D、二、填空题
-
5. 函数 的零点是6. 计算:
7. 已知 的展开式中含有 项的系数是54,则n=.
8. 掷一颗均匀的骰子,出现奇数点的概率为
9. 若 满足 ,则目标函数 的最大值是 .
10. 若复数 满足 ,则 的最大值是
11. 若一个圆锥的主视图(如图所示)是边长为3、3、2的三角形,则该圆锥的体积是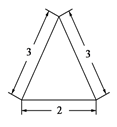 12. 若双曲线 ( )的左焦点在抛物线 的准线上,则 .
12. 若双曲线 ( )的左焦点在抛物线 的准线上,则 .
13. 若 ,则 的值为
14. 若 为等比数列, ,且 ,则 的最小值为
15. 在 中,角A、B、C所对的边分别为a、b、c , , .若 为钝角, ,则 的面积为
16. 已知非零向量 、 不共线,设 ,定义点集. 若对于任意的 ,当 , 且不在直线 上时,不等式 恒成立,则实数 的最小值为
三、解答题
-
17. 共享单车给市民出行带来了诸多便利,某公司购买了一批单车投放到某地给市民使用,
据市场分析,每辆单车的营运累计利润y(单位:元)与营运天数x 满足函数关系
式 .
(1)、要使营运累计利润高于800元,求营运天数的取值范围;(2)、每辆单车营运多少天时,才能使每天的平均营运利润 的值最大?18. 如图,在棱长为1的正方体 中,点E是棱AB上的动点. (1)、求证: ;(2)、若直线 与平面 所成的角是45 ,请你确定点E的位置,并证明你的结论.
(1)、求证: ;(2)、若直线 与平面 所成的角是45 ,请你确定点E的位置,并证明你的结论.
19. 已知数列 ,其前 项和为 ,满足 , ,其中 , , , .
(1)、若 , , ( ),求数列 的前 项和;
(2)、若 ,且 ,求证:数列 是等差数列.
20. 已知椭圆 ,直线 不过原点O且不平行于坐标轴, 与 有两个交点A、B , 线段AB的中点为M.
(1)、若 ,点K在椭圆 上, 、 分别为椭圆的两个焦点,求 的范围;(2)、证明:直线 的斜率与 的斜率的乘积为定值;(3)、若 过点 ,射线OM与 交于点P , 四边形 能否为平行四边形?若能,求此时 的斜率;若不能,说明理由.
21. 记函数 的定义域为D. 如果存在实数 、 使得 对任意满足 且 的x恒成立,则称 为 函数.(1)、设函数 ,试判断 是否为 函数,并说明理由;(2)、设函数 ,其中常数 ,证明: 是 函数;(3)、若 是定义在 上的 函数,且函数 的图象关于直线 (m为常数)对称,试判断 是否为周期函数?并证明你的结论.