福建省莆田仙游私立一中2016-2017学年八年级下学期数学期中考试试卷

试卷更新日期：2018-05-08 类型：期中考试

进入出卷网下载

一、单选题

1. 下列二次根式中，属于最简二次根式的是（）

A、 $\sqrt{\frac{1}{2}}$ B、 $\sqrt{5}$ C、 $\sqrt{4}$ D、 $\sqrt{0.8}$

查看试题解析
2. 二次根式 $\sqrt{x + 3}$ 有意义的条件是（）

A、x＞3 B、x＞﹣3 C、x≥3 D、x≥﹣3

查看试题解析
3. 下列y关于x的函数中，是正比例函数的为（）

A、y＝x² B、y＝ $\frac{2}{x}$ C、y＝ $\frac{x}{2}$ D、y＝ $\frac{x + 1}{2}$

查看试题解析
4. 化简 $\sqrt{（ - 2 ）^{2}}$ 的结果正确的是（）

A、﹣2 B、2 C、±2 D、4

查看试题解析
5. 平行四边形、矩形、菱形、正方形中是轴对称图形的有（）．

A、1个 B、2个 C、3个 D、4个

查看试题解析
6. 一次函数y=﹣2x+3的图象不经过的象限是（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
7. 下列说法中错误的是（）

A、两条对角线互相平分的四边形是平行四边形 B、两条对角线相等的四边形是矩形 C、两条对角线互相垂直的矩形是正方形 D、两条对角线相等的菱形是正方形

查看试题解析
8.
估计的值在（　　）

A、在1和2之间 B、在2和3之间 C、在3和4之间 D、在4和5之间

查看试题解析
9. 如图是一株美丽的勾股树，其中所有的四边形都是正方形，所有的三角形都是直角三角形．若正方形A，B，C，D的边长分别是3，5，2，3，则最大正方形E的面积是（）

A、13 B、26 C、47 D、94

查看试题解析
10. 如图，菱形ABCD的面积为120 $c m^{2}$ ，正方形AECF的面积为50 $c m^{2}$ ，则菱形的边长为（）

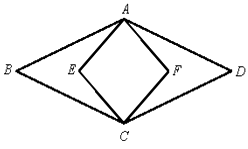A、12cm B、13cm C、14cm D、15cm

查看试题解析

二、填空题

11. 计算： $\sqrt{3}$ （ $\sqrt{3}$ + $\sqrt{27}$ ）= ．

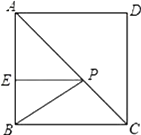
查看试题解析
12. 已知直线 $y = 2 x$ 向上平移一个单位长度后得到的直线是.

查看试题解析
13. $\sqrt{24 n}$ 是整数，则正整数n的最小值是．

查看试题解析
14. 如图，在正方形ABCD中，E是AB上一点，BE=2，AE=3，P是AC上一动点，则PB+PE的最小值是．

查看试题解析
15. 如图，在△ABC中，AB=10，∠B=60°，点D、E分别在AB、BC上，且BD=BE=4，将△BDE沿DE所在直线折叠得到△B′DE（点B′在四边形ADEC内），连接AB′，则AB′的长为．

查看试题解析
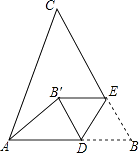16. 在平面直角坐标系中，直线l： $y = x - 1$ 与x轴交于点A₁ ，如图所示依次作正方形 $A_{1} B_{1} C_{1} O$ 、正方形 $A_{2} B_{2} C_{2} C_{1}$ 、…、正方形 $A_{n} B_{n} C_{n} C_{n - 1}$ ，使得点A₁、A₂、A₃、…在直线l上，点C₁、C₂、C₃、…在y轴正半轴上，则点 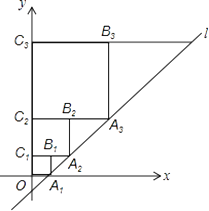$B_{2017}$ 的坐标是．

查看试题解析

三、解答题

17. 计算： $- 1^{2017} + {(- \frac{1}{2})}^{- 2} - \sqrt{\frac{1}{3}} \times \sqrt{48} + | 1 - \sqrt{2} | + {(π - 3)}^{0}$

查看试题解析
18. 已知正比例函数y=kx图象经过点（3，-6），求：

(1)、这个函数的解析式；

(2)、判断点A（4，-2）是否在这个函数图象上．

(3)、图象上的两点B（x₁ ， y₁）、C（x₂ ， y₂），如果x₁>x₂ ，比较y₁ ， y₂的大小.

查看试题解析
19. 如图，在四边形ABCD中，已知AB=3，BC=4，CD=12，AD=13，∠B=90°．求四边形ABCD的面积．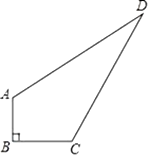

查看试题解析
20. 如图，点E是▱ABCD 边AD上一点，请你只用一把没有刻度的直尺，在BC边上确定一点F，使得CF=AE，请画出示意图，并用你学过的知识验证CF=AE。

查看试题解析
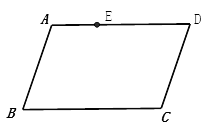21. 如图，在△ABC中，∠ACB= $90 °$ ，D，E分别为AC，AB的中点，BF∥CE交DE的延长线于点F.

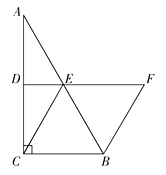(1)、求证：四边形ECBF是平行四边形；

(2)、当∠A= $30 °$ 时，求证：四边形ECBF是菱形.

查看试题解析
22. 已知：在Rt△ABC中，∠C＝90°，∠A、∠B、∠C的对边分别为a、b、c，设△ABC的面积为S，周长为l．

(1)、填表：
三边a、b、c
$a + b - c$
$\frac{S}{l}$
3、4、5
2

5、12、13
4

8、15、17
6

(2)、如果 $a + b - c = m$ ，观察上表猜想： $\frac{S}{l} =$ (用含有m的代数式表示)．

(3)、证明（2）中的结论．

查看试题解析
23. 如图，P为正方形ABCD的边BC上一动点(P与B. C不重合)，点Q在CD边上，且BP=CQ，连接AP、BQ交于点E，将△BQC沿BQ所在直线对折得到△BQN，延长QN交BA的延长线于点M.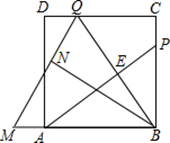

(1)、求证：AP⊥BQ；

(2)、若AB=3，BP=2PC，求QM的长；

(3)、当BP=m，PC=n时，求AM的长。

查看试题解析
24. 如图，在矩形ABCO中，点O为坐标原点，点B的坐标为（4，3），点A、C在坐标轴上，点P在BC边上，直线l₁：y=2x+3，直线l₂：y=2x﹣3．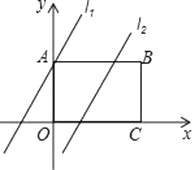

(1)、分别求直线l₁与x轴，直线l₂与AB的交点坐标；

(2)、已知点M在第一象限，且是直线l₂上的点，若△APM是等腰直角三角形，求点M的坐标；

查看试题解析

三边a、b、c	$a + b - c$	$\frac{S}{l}$
3、4、5	2
5、12、13	4
8、15、17	6