天津市东丽区2016-2017学年九年级上学期数学期末考试试卷
试卷更新日期:2018-05-08 类型:期末考试
一、单选题
-
1. 一个盒子装有除颜色外其它均相同的2个红球和3个白球,现从中任取1个球,则取到的是一个白球的概率为( )A、 B、 C、 D、2. 若关于 的一元二次方程 的一个根是 ,则 的值是( )A、 B、 C、 D、3. 下列图形中,是中心对称图形但不是轴对称图形的是( )A、
 B、
B、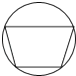 C、
C、 D、
D、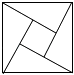 4. 抛物线 的顶点坐标是( )A、 B、 C、 D、5. 下列判断中正确的是( )A、长度相等的弧是等弧 B、平分弦的直线也必平分弦所对的两条弧 C、弦的垂直平分线必平分弦所对的两条弧 D、平分一条弧的直线必平分这条弧所对的弦6. 如图, 是⊙ 的弦,点 在圆上,已知 ,则 ( )
4. 抛物线 的顶点坐标是( )A、 B、 C、 D、5. 下列判断中正确的是( )A、长度相等的弧是等弧 B、平分弦的直线也必平分弦所对的两条弧 C、弦的垂直平分线必平分弦所对的两条弧 D、平分一条弧的直线必平分这条弧所对的弦6. 如图, 是⊙ 的弦,点 在圆上,已知 ,则 ( )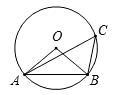 A、 B、 C、 D、7. 如图,在△ 中, ,将△ 绕点 顺时针旋转 ,得到△ ,连接 ,若 , ,则线段 的长为( )
A、 B、 C、 D、7. 如图,在△ 中, ,将△ 绕点 顺时针旋转 ,得到△ ,连接 ,若 , ,则线段 的长为( )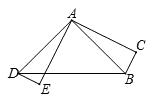 A、 B、 C、 D、8. 一元二次方程x2﹣4x+4=0的根的情况是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、无实数根 D、无法确定9. 已知抛物线 ,与 轴的一个交点为 ,则代数式 的值为( )A、 B、 C、 D、10. 已知等腰三角形的腰和底的长分别是一元二次方程 的根,则该三角形的周长是( )A、5 B、7 C、5或7 D、1011. 函数 中,当 时,函数值 的取值范围是( )A、 B、 C、 D、12. 已知△ 和△ 都是等腰直角三角形, , , , 是 的中点.若将△ 绕点 旋转一周,则线段 长度的取值范围是( )
A、 B、 C、 D、8. 一元二次方程x2﹣4x+4=0的根的情况是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、无实数根 D、无法确定9. 已知抛物线 ,与 轴的一个交点为 ,则代数式 的值为( )A、 B、 C、 D、10. 已知等腰三角形的腰和底的长分别是一元二次方程 的根,则该三角形的周长是( )A、5 B、7 C、5或7 D、1011. 函数 中,当 时,函数值 的取值范围是( )A、 B、 C、 D、12. 已知△ 和△ 都是等腰直角三角形, , , , 是 的中点.若将△ 绕点 旋转一周,则线段 长度的取值范围是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
13. 已知一元二次方程 的两根为 、 ,则14. 如图,在半径为 的⊙ 中,弦 , 于点 ,则
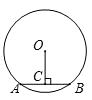 15. 已知二次函数 ,当x时, 随 的增大而减小.16. 圆内接正六边形的边心距为2 ,则这个正六边形的面积为 cm2 .17. 如图, 是半径为 的⊙ 的直径, 是圆上异于 , 的任意一点, 的平分线交⊙ 于点 ,连接 和 ,△ 的中位线所在的直线与⊙ 相交于点 、 ,则 的长是
15. 已知二次函数 ,当x时, 随 的增大而减小.16. 圆内接正六边形的边心距为2 ,则这个正六边形的面积为 cm2 .17. 如图, 是半径为 的⊙ 的直径, 是圆上异于 , 的任意一点, 的平分线交⊙ 于点 ,连接 和 ,△ 的中位线所在的直线与⊙ 相交于点 、 ,则 的长是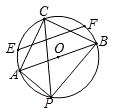 18. 如图所示的二次函数 的图象中,观察得出了下面五条信息:
18. 如图所示的二次函数 的图象中,观察得出了下面五条信息:① ;② ;③ ;④ ;⑤ ,
你认为其中正确信息的个数有个.

三、解答题
-
19. 解方程20. 如图,转盘A的三个扇形面积相等,分别标有数字1,2,3,转盘B的四个扇形面积相等,分别有数字1,2,3,4.转动A、B转盘各一次,当转盘停止转动时,将指针所落扇形中的两个数字相乘(当指针落在四个扇形的交线上时,重新转动转盘).
 (1)、用树状图或列表法列出所有可能出现的结果;(2)、求两个数字的积为奇数的概率.21. 如图,⊙ 是△ 的外接圆, 为直径,弦 , 交 的延长线于点 ,求证:
(1)、用树状图或列表法列出所有可能出现的结果;(2)、求两个数字的积为奇数的概率.21. 如图,⊙ 是△ 的外接圆, 为直径,弦 , 交 的延长线于点 ,求证: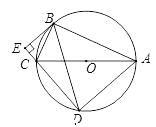 (1)、 ;(2)、 是⊙ 的切线.22. 已知:抛物线 经过 、 两点,顶点为 .求:(1)、求 , 的值;(2)、求△ 的面积.23. 如图,用长为 的铝合金条制成“日”字形窗框,若窗框的宽为 ,窗户的透光面积为 (铝合金条的宽度不计).
(1)、 ;(2)、 是⊙ 的切线.22. 已知:抛物线 经过 、 两点,顶点为 .求:(1)、求 , 的值;(2)、求△ 的面积.23. 如图,用长为 的铝合金条制成“日”字形窗框,若窗框的宽为 ,窗户的透光面积为 (铝合金条的宽度不计). (1)、求出 与 的函数关系式;(2)、如何安排窗框的长和宽,才能使得窗户的透光面积最大?并求出此时的最大面积.24. 如图1,已知 为正方形 的中心,分别延长 到点 , 到点 ,使 , ,连结 ,将△ 绕点 逆时针旋转 角得到△ (如图2).连结 、 .
(1)、求出 与 的函数关系式;(2)、如何安排窗框的长和宽,才能使得窗户的透光面积最大?并求出此时的最大面积.24. 如图1,已知 为正方形 的中心,分别延长 到点 , 到点 ,使 , ,连结 ,将△ 绕点 逆时针旋转 角得到△ (如图2).连结 、 .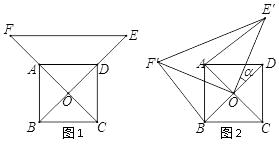 (1)、探究 与 的数量关系,并给予证明;(2)、当 , 时,求:① 的度数;② 的长度.25. 如图,抛物线 与 轴交于 、 两点(点 在点 的左侧),点 的坐标为 ,与 轴交于点 ,作直线 .动点 在 轴上运动,过点 作 轴,交抛物线于点 ,交直线 于点 ,设点 的横坐标为 .
(1)、探究 与 的数量关系,并给予证明;(2)、当 , 时,求:① 的度数;② 的长度.25. 如图,抛物线 与 轴交于 、 两点(点 在点 的左侧),点 的坐标为 ,与 轴交于点 ,作直线 .动点 在 轴上运动,过点 作 轴,交抛物线于点 ,交直线 于点 ,设点 的横坐标为 .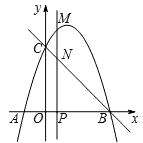 (1)、求抛物线的解析式和直线 的解析式;(2)、当点 在线段 上运动时,求线段 的最大值;(3)、当以 、 、 、 为顶点的四边形是平行四边形时,直接写出 的值.
(1)、求抛物线的解析式和直线 的解析式;(2)、当点 在线段 上运动时,求线段 的最大值;(3)、当以 、 、 、 为顶点的四边形是平行四边形时,直接写出 的值.