北京市东城区2016-2017学年七年级上学期数学期末考试试卷

试卷更新日期：2018-05-08 类型：期末考试

进入出卷网下载

一、单选题

1. ﹣8的相反数是（）

A、﹣8 B、8 C、- $\frac{1}{8}$ D、 $\frac{1}{8}$

查看试题解析
2. 某地一天的最高气温是8℃，最低气温是-2℃，则该地这天的温差是（）

A、10℃ B、-10℃ C、6℃ D、-6℃

查看试题解析
3. 我国于2016年9月15日成功发射天宫二号空间实验室．它是我国自主研发的第二个空间实验室，标志着我国即将迈入空间站时代．天宫二号空间实验室运行的轨道高度距离地球393000日，数据393000用科学记数法表示为（）

A、3.93×10⁶ B、39.3×10⁴ C、0.393×10⁶ D、3.93×10⁵

查看试题解析
4. 下列计算正确的是（）

A、x²＋x²＝x⁴ B、x²＋x³＝2x⁵ C、3x－2x＝1 D、x²y－2x²y＝－x²y

查看试题解析
5. 若代数式﹣5x⁶y³与2x²ⁿy³是同类项，则常数n的值（）

A、2 B、3 C、4 D、6

查看试题解析
6. 把下列图形折成正方体的盒子，折好后与“考”相对的字是（）

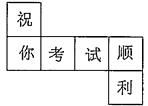A、祝 B、你 C、顺 D、利

查看试题解析
7.
如图，甲从A点出发向北偏东70°方向走到点B，乙从点A出发向南偏西15°方向走到点C，则∠BAC的度数是（　　）

A、85° B、160° C、125° D、105°

查看试题解析
8. 已知实数a、b在数轴上对应的点如图所示，则下列式子正确的是（）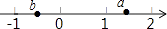

A、a•b＞0 B、a+b＜0 C、|a|＜|b| D、a﹣b＞0

查看试题解析
9. 关于 $x$ 的方程 $2 x + 5 a = 3$ 的解与方程 $2 x + 2 = 0$ 的解相同，则 $a$ 的值是（）

A、 $1$ B、 $4$ C、 $\frac{1}{5}$ D、 $- 1$

查看试题解析
10. 我国明代珠算家程大位的名著《直指算法统宗》里有一道著名算题：“一百馒头一百僧，大僧三个更无争，小僧三人分一个，大小和尚各几丁？”意思是：有100个和尚分100个馒头，如果大和尚1人分3个，小和尚3人分1个，正好分完，试问大、小和尚各多少人？设大和尚有x人，依题意列方程得（）

A、 $\frac{x}{3} + 3 (100 - x) = 100$ B、 $\frac{x}{3} - 3 (100 - x) = 100$ C、 $3 x + \frac{100 - x}{3} = 100$ D、 $3 x - \frac{100 - x}{3} = 100$

查看试题解析

二、填空题

11. 如图，从A地到B地共有五条路，人们常常选择第③条，请用几何知识解释原因．

查看试题解析
12. 如图所示，可以用量角器度量∠AOB的度数，那么∠AOB的余角度数为

查看试题解析
13. 如图所示的框图表示解方程3﹣5x=4﹣2x的流程，其中“系数化为1”这一步骤的依据是

查看试题解析
14. 写出一个解为 ${\begin{matrix} x = 1 \\ y = - 1 \end{matrix}$ 的二元一次方程是

查看试题解析
15. 计算 $(\frac{1}{4} + \frac{1}{6} - \frac{1}{2}) \times 12$ =

查看试题解析
16. 若代数式2x²﹣4x﹣5的值为7，则x²﹣2x﹣2的值为．

查看试题解析
17. 已知线段AB=8，在直线AB上取一点P，恰好使 $\frac{A P}{P B}$ =3，点Q为线段PB的中点．则AQ的长为

查看试题解析
18. 如图，用相同的小正方形按照某种规律进行摆放，则第6个图形中小正方形的个数是，第n（n为正整数）个图形中小正方形的个数是（用含n的代数式表示）．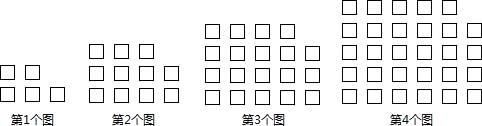

查看试题解析

三、解答题

19. 计算：

(1)、|-12|-（-15）+（-24）× $\frac{1}{6}$

(2)、-1²×2+（-2）²÷4-（-3）．

查看试题解析
20. 解方程

(1)、3（x﹣2）=x﹣4

(2)、 $\frac{x + 1}{2} - 1 = \frac{2 - x}{3}$ ．

查看试题解析
21. 解方程组

(1)、 ${\begin{matrix} x = 3 + y \\ 3 x - 2 y = 5 \end{matrix}$ ；

(2)、 ${\begin{matrix} 2 x + 3 y = 7 \\ 3 x + 2 y = 3 \end{matrix}$ ．

查看试题解析
22. 先化简，再求值：3（2x²y-xy²）-（5x²y+2xy²），其中|x+1|+（y﹣2）²=0．

查看试题解析
23. 根据下列语句，画出图形．

(1)、如图1，已知四点A，B，C，D．
①画直线AB；
②连接线段AC、BD，相交于点O；
③画射线AD，BC，交于点P．

(2)、如图2，已知线段a，b，作一条线段，使它等于2a﹣b（不写作法，保留作图痕迹）．

查看试题解析
24. （列方程解应用题）互联网“微商”经营已成为大众创业新途径，某微信平台上一件商品进价为180元，按标价的八折销售，仍可获利60元，求这件商品的标价．

查看试题解析
25. 阅读材料，对于任何数，我们规定符号 $| \begin{matrix} a \\ c \end{matrix}$ $\begin{matrix} b \\ d \end{matrix} |$ 的意义是： $| \begin{matrix} a \\ c \end{matrix}$ $\begin{matrix} b \\ d \end{matrix} |$ =ad﹣bc，例如： $| \begin{matrix} 1 \\ 3 \end{matrix}$ $\begin{matrix} 2 \\ 4 \end{matrix} |$ =1×4﹣2×3=﹣2．

(1)、按照这个规定，请你计算 $| \begin{matrix} 5 \\ 2 \end{matrix}$ $\begin{matrix} 6 \\ 4 \end{matrix} |$ 的值．

(2)、按照这个规定，当 $| \begin{matrix} 2 x - 1 \\ x + 2 \end{matrix}$ $\begin{matrix} - 2 \\ \frac{1}{2} \end{matrix} |$ =5时，求x的值．

查看试题解析
26. 如图①，O是直线AB上的一点，∠COD是直角，OE平分∠BOC．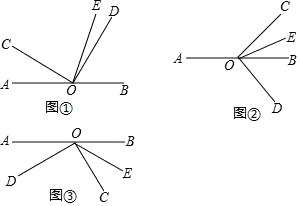

(1)、若∠AOC=30°时，则∠DOE的度数为

(2)、将图①中的∠COD绕顶点O顺时针旋转至图②的位置，其它条件不变，探究∠AOC和∠DOE的度数之间的关系，写出你的结论，并说明理由；

(3)、将图①中的∠COD绕顶点O顺时针旋转至图③的位置，其他条件不变．直接写出∠AOC和∠DOE的度数之间的关系：

查看试题解析
27. 某水果批发市场苹果的价格如表
购买苹果（千克）
不超过20千克
20千克以上但不超过40千克
40千克以上
每千克的价格
6元
5元
4元

(1)、小明分两次共购买40千克，第二次购买的数量多于第一次购买的数量，共付出216元，小明第一次购买苹果千克，第二次购买千克．

(2)、小强分两次共购买100千克，第二次购买的数量多于第一次购买的数量，且两次购买每千克苹果的单价不相同，共付出432元，请问小强第一次，第二次分别购买苹果多少千克？（列方程解应用题）

查看试题解析

购买苹果（千克）	不超过20千克	20千克以上但不超过40千克	40千克以上
每千克的价格	6元	5元	4元