北京市丰台区2016-2017学年八年级下学期数学期中考试试卷
试卷更新日期:2018-05-08 类型:期中考试
一、单选题
-
1. 在平面直角坐标中,点P(-3, 5)关于原点的对称点在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限2. 下列环保标志中,是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 如果一个多边形的内角和等于720°,那么这个多边形是( ).
3. 如果一个多边形的内角和等于720°,那么这个多边形是( ).
A、四边形 B、五边形 C、六边形 D、七边形4. 下列各曲线表示的y与x的关系中,y不是x的函数的是( )A、 B、
B、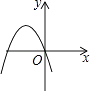 C、
C、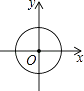 D、
D、 5. 点A(-1,m),B(2016,n)在一次函数y = -x+2017的图象上,则( )A、 B、 C、 D、m、n的大小关系不确定.6. 下列关于正比例函数y = 3x的说法中,正确的是( )A、当x=3时,y =1 B、它的图象是一条过原点的直线 C、y随x的增大而减小 D、它的图象经过第二、四象限7. 已知,在平面直角坐标系xOy中,点A( -4,0 ),点B在直线y = x+2上.当A,B两点间的距离最小时,点B的坐标是( )A、( , ) B、( , ) C、( -3,-1 ) D、(-3, )8. 菱形ABCD的对角线AC=6,BD=8,那么边AB的长度 是( )A、10 B、5 C、 D、9. 如图,在菱形 中, =120°,点E是边 的中点,P是对角线 上的一个动点,若AB=2,则PB+PE的最小值是( )
5. 点A(-1,m),B(2016,n)在一次函数y = -x+2017的图象上,则( )A、 B、 C、 D、m、n的大小关系不确定.6. 下列关于正比例函数y = 3x的说法中,正确的是( )A、当x=3时,y =1 B、它的图象是一条过原点的直线 C、y随x的增大而减小 D、它的图象经过第二、四象限7. 已知,在平面直角坐标系xOy中,点A( -4,0 ),点B在直线y = x+2上.当A,B两点间的距离最小时,点B的坐标是( )A、( , ) B、( , ) C、( -3,-1 ) D、(-3, )8. 菱形ABCD的对角线AC=6,BD=8,那么边AB的长度 是( )A、10 B、5 C、 D、9. 如图,在菱形 中, =120°,点E是边 的中点,P是对角线 上的一个动点,若AB=2,则PB+PE的最小值是( ) A、1 B、 C、2 D、10. 如图,矩形ABCD中,对角线AC、BD相交于点O,E、F分别是边BC、AD的中点,AB=2,BC=4,一动点P从点B出发,沿着B—A—D—C的方向在矩形的边上运动,运动到点C停止.点M为图1中的某个定点,设点P运动的路程为x,△BPM的面积为y,表示y与x的函数关系的图象大致如图2所示.那么,点M的位置可能是图1中的( )
A、1 B、 C、2 D、10. 如图,矩形ABCD中,对角线AC、BD相交于点O,E、F分别是边BC、AD的中点,AB=2,BC=4,一动点P从点B出发,沿着B—A—D—C的方向在矩形的边上运动,运动到点C停止.点M为图1中的某个定点,设点P运动的路程为x,△BPM的面积为y,表示y与x的函数关系的图象大致如图2所示.那么,点M的位置可能是图1中的( ) A、点 C B、点E C、点F D、点O
A、点 C B、点E C、点F D、点O二、填空题
-
11. 函数 的自变量x的取值范围是 .
12. 园林队在某公园进行绿化,中间休息了一段时间.已知绿化面积s与工作时间t的函数关系如图所示,则休息后园林队每小时绿化面积为平方米 13. 四边形ABCD中,已知∠A=∠B = ∠C = 90°,再添加一个条件,使得四边形ABCD为正方形,可添加的条件是(答案不唯一,只添加一个即可).
13. 四边形ABCD中,已知∠A=∠B = ∠C = 90°,再添加一个条件,使得四边形ABCD为正方形,可添加的条件是(答案不唯一,只添加一个即可).
14. 四边形ABCD中,点E、F、G、H分别为AB、BC、CD、DA边的中点,顺次连接各边中点得到的新四边形EFGH称为中点四边形;画图猜想:无论四边形ABCD怎样变化,它的中点四边形EFGH都是四边形。当满足以下条件时;①当对角线AC=BD时,四边形ABCD的中点四边形为形;
②当对角线AC⊥BD时,四边形ABCD的中点四边形是形。
15. 已知一次函数 的图象经过第一、三、四象限,请你赋予k和b具体的数值,写出一个符合条件的表达式.
16. 阅读下面材料:在数学课上,老师提出如下问题:
尺规作图:过直线外一点作已知直线的平行线
已知:直线l及其外一点A
求作:l的平行线,使它经过点A

小云的作法如下:
⑴在直线l上任取两点B,C;
⑵以A为圆心,以BC长为半径作弧以C为圆心,AB长为半径作弧两弧相交于点D
⑶作直线AD,直线AD即为所求

老师说:“小云的作法正确.”请回答:小云的作图依据是
三、解答题
-
17. 已知一次函数的图象经过点(-1,-5),且与正比例函数y= x的图象相交于点(2,a).求这个一次函数的图象与x轴的交点坐标及与坐标轴围成的三角形的面积。
18. 如图,AC=BC,D是AB中点,CE//AB,CE=AB. (1)、求证:四边形CDBE是矩形.(2)、若AC=5,CD=3,F是BC上一点,且DF⊥BC.求DF的长.19. 如图,在平面直角坐标系中,一次函数 的图象与 x轴交点为A,与y轴交点为B,且与正比例函数 的图象的交于点C(m,4) .
(1)、求证:四边形CDBE是矩形.(2)、若AC=5,CD=3,F是BC上一点,且DF⊥BC.求DF的长.19. 如图,在平面直角坐标系中,一次函数 的图象与 x轴交点为A,与y轴交点为B,且与正比例函数 的图象的交于点C(m,4) . (1)、求m的值及一次函数 的表达式;
(1)、求m的值及一次函数 的表达式;
(2)、若点P是y轴上一点,且△BPC的面积为6,请直接写出点P的坐标。
20. 如图,在矩形纸片ABCD中,AD=5,AB=3, 点 为 上一点,沿着AE剪下 ,将它平移至 的位置,拼成四边形 . (1)、当点E与点B的距离是多少时,四边形 是菱形?并说明理由;
(1)、当点E与点B的距离是多少时,四边形 是菱形?并说明理由;
(2)、在(1)的条件下,求菱形 的两条对角线的长.
21. 如图,已知直线AB 的函数表达式为 ,与 x轴交点为A,与y轴交点为B. (1)、求 A , B两点的坐标;(2)、若点P为线段AB上的一个动点,作 PE⊥y轴于点E,PF⊥x轴于点F,连接EF.是否存在点P,使EF 的值最小?若存在,求出EF 的最小值;若不存在,请说明理由。22. 某工厂现有甲种原料360千克,乙种原料290千克,计划利用这两种原料生产A、B两种产品共50件.已知生产一件A种产品需用甲种原料9千克、乙种原料3千克,可获利润700元;生产一件B种产品需用甲种原料4千克、乙种原料10千克,可获利润1200元。设生产A种产品的生产件数为x, A、B两种产品所获总利润为y (元)
(1)、求 A , B两点的坐标;(2)、若点P为线段AB上的一个动点,作 PE⊥y轴于点E,PF⊥x轴于点F,连接EF.是否存在点P,使EF 的值最小?若存在,求出EF 的最小值;若不存在,请说明理由。22. 某工厂现有甲种原料360千克,乙种原料290千克,计划利用这两种原料生产A、B两种产品共50件.已知生产一件A种产品需用甲种原料9千克、乙种原料3千克,可获利润700元;生产一件B种产品需用甲种原料4千克、乙种原料10千克,可获利润1200元。设生产A种产品的生产件数为x, A、B两种产品所获总利润为y (元)
(1)、试写出y与x之间的函数关系式;(2)、求出自变量x的取值范围;
(3)、利用函数的性质说明哪种生产方案获总利润最大?最大利润是多少?
23. 小东根据学习一次函数的经验,对函数y 的图象和性质进行了探究.下面是小东的探究过程,请补充完成:(1)、函数y 的自变量x的取值范围是;(2)、已知:①当 时, ; ②当x> 时,③当x< 时, ;显然,②和③均为某个一次函数的一部分.
(3)、由(2)的分析,取5个点可画出此函数的图象,请你帮小东确定下表中第5个点的坐标(m,n),其中m=;n=;x
…
-2
0
1
m
…
y
…
5
1
0
1
n
…
(4)、在平面直角坐标系XOY中,做出函数y 的图象: (5)、根据函数的图象,写出函数y 的一条性质;24. 已知:如图,在正方形ABCD中,M,N分别是边AD,CD上的点,且∠MBN=45°,连接MN。
(5)、根据函数的图象,写出函数y 的一条性质;24. 已知:如图,在正方形ABCD中,M,N分别是边AD,CD上的点,且∠MBN=45°,连接MN。求证:MN=AM+CN.
 25. 如图,点O为正方形ABCD的对角线交点,将线段OE绕点O逆时针方向旋转 ,点E的对应点为点F,连接EF,AE,BF.
25. 如图,点O为正方形ABCD的对角线交点,将线段OE绕点O逆时针方向旋转 ,点E的对应点为点F,连接EF,AE,BF. (1)、请依题意补全图形;
(1)、请依题意补全图形;
(2)、根据补全的图形,猜想并证明直线AE与BF的位置关系.
26. 在正方形 中,点 是边 上一个动点,连结 , ,点 , 分别为 , 的中点,连结 交直线 于点E. (1)、如图1,当点 与点 重合时, 的形状是;(2)、当点 在点M的左侧时,如图2.
(1)、如图1,当点 与点 重合时, 的形状是;(2)、当点 在点M的左侧时,如图2.①依题意补全图2;
②判断 的形状,并加以证明.
27. 在学习了正方形后,数学小组的同学对正方形进行了探究,发现:
图1 图2 图3
(1)、如图1,在正方形ABCD中,点E为BC边上任意一点(点E不与B、C重合),点F在线段AE上,过点F的直线MN⊥AE,分别交AB、CD于点M、N . 此时,有结论AE=MN,请进行证明;(2)、如图2:当点F为AE中点时,其他条件不变,连接正方形的对角线BD, MN 与BD交于点G,连接BF,此时有结论:BF= FG,请利用图2做出证明.(3)、如图3:当点E为直线BC上的动点时,如果(2)中的其他条件不变,直线MN分别交直线AB、CD于点M、N,请你直接写出线段AE与MN之间的数量关系、线段BF与FG之间的数量关系.28. 已知四边形ABCD是正方形,点E、F分别在射线AB、射线BC上,AE=BF,DE与AF交于点O. (1)、如图1,当点E、F分别在线段AB、BC上时,则线段DE与线段AF的数量关系是 , 位置关系是
(1)、如图1,当点E、F分别在线段AB、BC上时,则线段DE与线段AF的数量关系是 , 位置关系是
(2)、将线段AE沿AF进行平移至FG,连结DG.①如图2,当点E在AB延长线上时,补全图形,写出AD,AE,DG之间的数量关系.
②若DG= , ,直接写出AD长.
29. 如图,在平面直角坐标系中,已知点A(2,3)、B(6,3),连接AB.如果对于平面内一点P,线段AB上都存在点Q,使得PQ≤1,那么称点P是线段AB的“附近点”. (1)、请判断点D(4.5,2.5)是否是线段AB的“附近点”;
(1)、请判断点D(4.5,2.5)是否是线段AB的“附近点”;
(2)、如果点H (m,n)在一次函数 的图象上,且是线段AB的“附近点”,求m的取值范围;
(3)、如果一次函数 的图象上至少存在一个“附近点”,请直接写出b的取值范围.
30. 已知菱形OABC在坐标系中的位置如图所示, O是坐标原点,点C ,点A在x轴上,点M(0,2)。
 (1)、点P是直线OB 上的动点,求PM+PC最小值.
(1)、点P是直线OB 上的动点,求PM+PC最小值.
(2)、将直线 向上平移,得到直线 .①当直线y=kx+b与线段OC有公共点时,结合图象,直接写出b的取值范围.
②当直线y=kx+b将四边形OABC分成面积相等的两部分时,求k,b。
(只需写出解题的主要思路,不用写出计算结果).