北京市东城五中分校2016-2017学年八年级下学期数学期中考试试卷

试卷更新日期：2018-05-08 类型：期中考试

进入出卷网下载

一、单选题

1. 若关于的 $x$ 方程 $x^{2} + 3 x + a = 0$ 有一个根为 $- 1$ ，则 $a$ 的值为（）．

A、 $- 4$ B、 $- 2$ C、 $2$ D、 $4$

查看试题解析
2. 二次函数 $y = - x^{2} + 2 x + 4$ 的最大值为（）

A、3 B、4 C、5 D、6

查看试题解析
3. 在平面直角坐标系 $x O y$ 中，点 $A$ 的坐标为 $(- 1 ， 2)$ ， $A B ⊥ x$ 轴于点 $B$ ，以原点 $O$ 为位似中心，将 $△ O A B$ 放大为原来的 $2$ 倍，得到 $△ O A_{1} B_{1}$ ，且点 $A_{1}$ 在第二象限，则点 $A_{1}$ 的坐标为（）．

A、 $(- 2 ， 4)$ B、 $(- \frac{1}{2} ， 1)$ C、 $(2 ， - 4)$ D、 $(2 ， 4)$

查看试题解析
4. 在平面直角坐标系中，点 $B$ 的坐标为 $(3 ， 1)$ ，则点 $B$ 关于原点的对称点的坐标为（）．

A、 $(3 ， - 1)$ B、 $(- 3 ， 1)$ C、 $(- 1 ， - 3)$ D、 $(- 3 ， - 1)$

查看试题解析
5. 某学校组织学生进行社会主义核心价值观的知识竞赛，进入决赛的共有20名学生，他们的决赛成绩如下表所示：
决赛成绩/分
95
90
85
80
人数
4
6
8
2
那么20名学生决赛成绩的众数和中位数分别是（　　）

A、85，90 B、85，87.5 C、90，85 D、95，90

查看试题解析
6. 若二次函数 $y = x^{2} + b x$ 的图象的对称轴是经过点(2，0)且平行于y轴的直线，则关于x的方程 $x^{2} + b x = 5$ 的解为（）

A、 $x_{1} = 0, x_{2} = 4$ B、 $x_{1} = 1, x_{2} = 5$ C、 $x_{1} = 1, x_{2} = - 5$ D、 $x_{1} = - 1, x_{2} = 5$

查看试题解析
7. 如图，在 $△ A B C$ 中， $D E ∥ B C$ ， $A D = 6$ ， $D B = 3$ ，则 $\frac{S_{△ A D E}}{S_{△ A B C}}$ 的值为（）．

A、 $\frac{1}{2}$ B、 $\frac{2}{3}$ C、 $\frac{4}{5}$ D、 $\frac{4}{9}$

查看试题解析
8. 如图，点 $D$ ， $E$ 分别在 $△ A B C$ 的 $A B$ ， $A C$ 边上，增加下列条件中的一个：
① $∠ A E D = ∠ 8$ ，② $∠ A D E = ∠ C$ ，③ $\frac{A E}{A B} = \frac{D E}{B C}$ ，④ $\frac{A D}{A C} = \frac{A E}{A B}$ ，⑤ $A C^{2} = A D \cdot A E$ ，使 $△ A D E$ 与 $△ A C B$ 一定相似的有（）．

A、①②④ B、②④⑤ C、①②③④ D、①②③⑤

查看试题解析
9. 如图，在 $Rt △ A B C$ 中， $∠ A C B = 90 °$ ， $D$ 为斜边 $A B$ 的中点，动点 $P$ 从 $B$ 点出发，沿 $B \to C \to A$ 运动，如图 $1$ 所示，设 $S_{△ D P B} = y$ ，点 $P$ 运动的路程为 $x$ ，若 $y$ 与 $x$ 之间的函数图象如图 $2$ 所示，则 $△ A B C$ 的面积为（）．

A、 $4$ B、 $6$ C、 $12$ D、 $14$

查看试题解析
10. 二次函数 $y = 2 x^{2} - 8 x + m$ 满足以下条件：当 $- 2 < x < - 1$ 时，它的图像位于 $x$ 轴的下方；当 $6 < x < 7$ 时，它的图像位于 $x$ 轴的上方，则 $m$ 的值为（）．

A、 $8$ B、 $- 10$ C、 $- 42$ D、 $- 24$

查看试题解析

二、填空题

11. 将抛物线 $y = x^{2} - 2 x + 3$ 向上平移 $2$ 个单位长度，再向右平移 $3$ 个单位长度后得到的抛物线的解析式为．

查看试题解析
12. 若 $\frac{a}{b} = \frac{3}{4}$ ，则 $\frac{a + b}{b}$ 的值为

查看试题解析
13. $△ A B C$ 的三边长分别为 $5$ ， $12$ ， $13$ ，与它相似的 $△ D E F$ 的最小边长为 $15$ ，则 $△ D E F$ 的周长为．

查看试题解析
14. 如图，矩形 $A B C D$ 中，点 $E$ 是边 $A D$ 的中点， $B E$ 交对角线 $A C$ 于点 $F$ ，则 $△ A F E$ 与 $△ B C F$ 的面积比等于．

查看试题解析
15. 如图是跷跷板的示意图，立柱 $O C$ 与地面垂直，以 $O$ 为横板 $A B$ 的中点， $A B$ 绕点 $O$ 上下转动，横板 $A B$ 的 $B$ 端最大高度 $h$ 是否会随横板长度的变化而变化呢？一位同学做了如下研究：他先设 $A B = 2 m$ ， $O C = 0.5 m$ ，通过计算得到此时的 $h_{1}$ ，再将横板 $A B$ 换成横板 $A^{'} B^{'}$ ， $O$ 为横板 $A^{'} B^{'}$ 的中点，且 $A^{'} B^{'} = 3 m$ ，此时 $B^{'}$ 点的最大高度为 $h_{2}$ ，由此得到 $h_{1}$ 与 $h_{2}$ 的大小关系是： $h_{1}$ $h_{2}$ （填“ $>$ 、“ $=$ ”或“ $<$ ”）可进一步得出， $h$ 随横板的长度的变化而（填“不变”或“改变”）．

查看试题解析
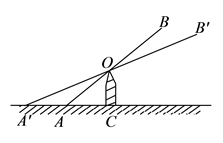16. 如果一个平行四边形一个内角的平分线分它的一边为1∶2的两部分，那么称这样的平行四边形为“协调平行四边形”，称该边为“协调边”。当“协调边”为3时，它的周长为.

查看试题解析

三、解答题

17. 计算

(1)、分解因式 $2 m x^{2} - 3 m x + x - 2 m - 2$ ．

(2)、解方程： $x^{2} - 6 x - 1 = 0$ ．

查看试题解析
18. 如图， $△ A B C$ 中， $D$ 为 $B C$ 上一点， $∠ B A D = ∠ C$ ， $A B = 6$ ， $B D = 4$ ，求 $C D$ 的长．

查看试题解析
19. 已知：抛物线 $y = x^{2} + (2 m - 1) x + m^{2} - 1$ 经过坐标原点，且当 $x < 0$ 时， $y$ 随 $x$ 的增大而减小．

(1)、求抛物线的解析式．

(2)、结合图像写出 $y < 0$ 时，对应的 $x$ 的取值范围．

(3)、设点 $A$ 是该抛物线上位于 $x$ 轴下方的一个动点，过点 $A$ 作 $x$ 轴的平行线交抛物线于另一点 $D$ ，再作 $A B ⊥ x$ 轴于点 $B$ ， $D C ⊥ x$ 轴于点 $C$ ，当 $B C = 1$ 时，直接写出矩形 $A B C D$ 的周长．

查看试题解析
20. 如图，在平面直角坐标系 $x O y$ 中，正比例函数 $y = 2 x$ 与反比例函数 $y = \frac{k}{x}$ 的图像交于 $A$ 、 $B$ 两点，点 $A$ 的横坐标为 $2$ ， $A C ⊥ x$ 轴于点 $C$ ，连接 $B C$ ．

(1)、求反比例函数的表达式．

(2)、若点 $P$ 是反比例函数 $y = \frac{k}{x}$ 图像上一点，且满足 $△ O P C$ 的面积是 $△ A B C$ 面积的一半，请直接写出点 $P$ 的坐标．

查看试题解析
21. 列方程或方程组解应用题：
某公司在2013年的盈利额为200万元，预计2015年的盈利额将达到242万元，若每年比上一年盈利额增长的百分率相同，求该公司这两年盈利额的年平均增长率是多少？

查看试题解析
22. 如图，四边形 $A B C D$ 中， $B D$ 垂直平分 $A C$ ，垂足为点 $F$ ， $E$ 为四边形 $A B C D$ 外一点，且 $∠ A D E = ∠ B A D$ ， $A E ⊥ A C$ ．

(1)、求证：四边形 $A B D E$ 是平行四边形．

(2)、如果 $D A$ 平分 $∠ B D E$ ， $A B = 5$ ， $A D = 6$ ，求 $A C$ 的长．

查看试题解析
23. 在平面直角坐标系 $x O y$ 中，抛物线 $y = m x^{2} - 8 m x + 16 m - 1 (m > 0)$ 与 $x$ 轴的交点分别为 $A (x_{1} ， 0)$ ， $B (x_{2} ， 0)$ ．

(1)、求证：抛物线总与 $x$ 轴有两个不同的交点．

(2)、若 $A B = 2$ ，求此抛物线的解析式．

(3)、已知 $x$ 轴上两点 $C (2 ， 0)$ ， $D (5 ， 0)$ ，若抛物线 $y = m x^{2} - 8 m x + 16 m - 1 (m > 0)$ 与选段 $C D$ 有交点，请写出 $m$ 的取值范围．

查看试题解析
24. 在菱形 $A B C D$ 中， $∠ A B C = 60 °$ ， $E$ 是对角线 $A C$ 上任意一点， $F$ 是线段 $B C$ 延长线上一点，且 $C F = A E$ ，连接 $B E$ 、 $E F$ ．

(1)、如图 $1$ ，当 $E$ 是线段 $A C$ 的中点时，易证 $B E = E F$ ．

(2)、如图 $2$ ，当点 $E$ 不是线段 $A C$ 的中点，其它条件不变时，请你判断（ $1$ ）中的结论：（填“成立”或“不成立”）．

(3)、如图 $3$ ，当点 $E$ 不是线段 $A C$ 延长线上的任意一点，其它条件不变时，（ $1$ ）中的结论是否成立？若成立，请给予证明：若不成立，请说明理由．

查看试题解析
25. 已知两个函数，如果对于任意的自变量 $x$ ，这两个函数对应的函数值记为 $y_{1}$ ， $y_{2}$ ，都有点 $(x ， y_{1})$ 、 $(x ， y_{2})$ 关于点 $(x ， x)$ 对称，则称这两个函数为关于 $y = x$ 的对称函数，例如， $y_{1} = \frac{1}{2} x$ 和 $y_{2} = \frac{3}{2} x$ 为关于 $y = x$ 的对称函数，

(1)、判断：① $y_{1} = 3 x$ 和 $y_{2} = x$ ；② $y_{1} = x + 1$ 和 $y_{2} = x - 1$ ；③ $y_{1} = x^{2} + 1$ 和 $y_{2} = x^{2} - 1$ ，其中为关于 $y = x$ 的对称函数的是（填序号）．

(2)、若 $y_{1} = 3 x + 2$ 和 $y_{2} = k x + b (k \neq 0)$ 为关于 $y = x$ 的对称函数．
①求 $k$ 、 $b$ 的值．

(3)、若 $y_{1} = a x^{2} + b x + c (a \neq 0)$ 和 $y_{2} = x^{2} + n$ 为关于 $y = x$ 对称函数，且对于任意的实数 $x$ ，都有 $y_{1} < y_{2}$ ，请结合函数的图象，求 $n$ 的取值范围．

查看试题解析

决赛成绩/分	95	90	85	80
人数	4	6	8	2