2016-2017学年河南省郑州市七校联考高二上学期期中数学试卷（理科）

试卷更新日期：2016-12-15 类型：期中考试

进入出卷网下载

一、选择题

1. 已知a＞b，c＞d，且c，d不为0，那么下列不等式一定成立的是（）

A、ad＞bc B、ac＞bd C、a﹣c＞b﹣d D、a+c＞b+d

查看试题解析
2. 不等式（x﹣1）（2﹣x）≥0的解集为（　　）

A、{x|1≤x≤2} B、{x|x≤1或x≥2} C、{x|1＜x＜2} D、{x|x＜1或x＞2}

查看试题解析
3. 在数列{a_n}中，若a₁=﹣2，且对任意的n∈N^*有2a_n₊₁=1+2a_n ，则数列{a_n}前10项的和为（）

A、2 B、10 C、 $\frac{5}{2}$ D、 $\frac{5}{4}$

查看试题解析
4. 已知等比数列{a_n}满足a₁=3，a₁+a₃+a₅=21，则a₃+a₅+a₇=（）

A、21 B、42 C、63 D、84

查看试题解析
5. 在△ABC中，a=x，b=2，B=45°，若此三角形有两解，则x的取值范围是（）

A、x＞2 B、x＜2 C、 $2 ＜ x ＜ 2 \sqrt{2}$ D、 $2 ＜ x ＜ 2 \sqrt{3}$

查看试题解析
6. 在△ABC中，A=60°，AB=2，且△ABC的面积为 $\frac{\sqrt{3}}{2}$ ，则BC的长为（）

A、 $\frac{\sqrt{3}}{2}$ B、 $\sqrt{3}$ C、2 $\sqrt{3}$ D、2

查看试题解析
7. 若关于x的不等式x+ $\frac{4}{x}$ ≥a²﹣3a对任意实数x＞0恒成立，则实数a的取值范围为（）

A、[﹣1，4] B、（﹣∞，﹣2]∪[5，+∞） C、（﹣∞，﹣1]∪[4，+∞） D、[﹣2，5]

查看试题解析
8. 若变量x，y满足约束条件 ${\begin{matrix} y \leq x \\ x + y \leq 1 \\ y \geq - 1 \end{matrix}$ ，且z=2x+y的最大值和最小值分别为m和n，则m﹣n=（）

A、5 B、6 C、7 D、8

查看试题解析
9.
如图，从气球A上测得正前方的河流的两岸B，C的俯角分别为75°，30°，此时气球的高是60m，则河流的宽度BC等于（）

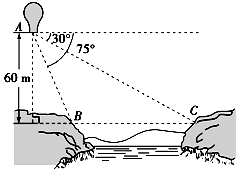A、 $30 (\sqrt{3} + 1)$ m B、 $120 (\sqrt{3} - 1)$ m C、 $180 (\sqrt{2} - 1)$ m D、 $240 (\sqrt{3} - 1)$ m

查看试题解析
10. 在△ABC中，角A，B，C的对边分别为a，b，c，若A，B，C成等差数列，2a，2b，2c成等比数列，则cosAcosB=（）

A、 $\frac{1}{4}$ B、 $\frac{1}{6}$ C、 $\frac{1}{2}$ D、 $\frac{2}{3}$

查看试题解析
11. 已知数列{a_n}： $\frac{1}{2}$ ， $\frac{1}{3}$ + $\frac{2}{3}$ ， $\frac{1}{4}$ + $\frac{2}{4}$ + $\frac{3}{4}$ ，…， $\frac{1}{10}$ + $\frac{2}{10}$ + $\frac{3}{10}$ +…+ $\frac{9}{10}$ ，…，若b_n= $\frac{1}{a_{n} \cdot a_{n + 1}}$ ，那么数列{b_n}的前n项和S_n为（）

A、 $\frac{n}{n + 1}$ B、 $\frac{4 n}{n + 1}$ C、 $\frac{3 n}{n + 1}$ D、 $\frac{5 n}{n + 1}$

查看试题解析
12. 已知各项均为正数的等比数列{a_n}满足a₇=a₆+2a₅ ，若存在两项a_m ， a_n使得 $\sqrt{a_{m} a_{n}}$ =4a₁ ，则 $\frac{1}{m}$ + $\frac{4}{n}$ 的最小值为（）

A、 $\frac{3}{2}$ B、 $\frac{5}{3}$ C、 $\frac{9}{4}$ D、 $\frac{25}{6}$

查看试题解析

二、填空题

13. 已知数列{a_n}中，a₁=1且 $\frac{1}{a_{n + 1}}$ = $\frac{1}{a_{n}}$ + $\frac{1}{3}$ （n∈N^*），则a₁₀= ．

查看试题解析
14. 在△ABC中，角A，B，C的对边分别为a，b，c，已知bcosC+ $\sqrt{3}$ bsinC﹣a﹣c=0，则角B= ．

查看试题解析
15. 设实数x，y满足约束条件 ${\begin{matrix} 3 x - y - 6 \leq 0 \\ x - y + 2 \geq 0 \\ x \geq 0 \\ y \geq 0 \end{matrix}$ ，若目标函数z=ax+by（a＞0，b＞0）的最大值为10，则a²+b²的最小值为．

查看试题解析
16. 意大利著名数学家斐波那契在研究兔子繁殖问题时，发现有这样一列数：1，1，2，3，5，8，13，…，其中从第三个数起，每一个数都等于它前面两个数的和，人们把这样的一列数所组成的数列{a_n}称为“斐波那契数列”，该数列是一个非常美丽、和谐的数列，有很多奇妙的属性，比如：随着项数的增加，前一项与后一项的比值越逼近黄金分割.06180339887．若把该数列{a_n}的每一项除以4所得的余数按相对应的顺序组成新数列{b_n}，在数列{b_n}中第2016项的值是．

查看试题解析

三、解答题：解答应写出文字说明，证明过程或演算步骤.

17. 已知关于x的不等式kx²﹣2x+3k＜0．

(1)、若不等式的解集为{x|x＜﹣3或x＞﹣1}，求k的值；

(2)、若不等式的解集为∅，求实数k的取值范围．

查看试题解析
18. 在△ABC中，内角A，B，C的对边分别为a，b，c．已知 $\frac{\cos A - 2 \cos C}{\cos B} = \frac{2 c - a}{b}$ ．

(1)、求 $\frac{\sin C}{\sin A}$ 的值；

(2)、若cosB= $\frac{1}{4}$ ，△ABC的周长为5，求b的长．

查看试题解析
19. 已知数列{a_n}的前n项和S_n= $\frac{n^{2} + n}{2}$ ，n∈N^* ．

(1)、求数列{a_n}的通项公式；

(2)、设b_n=2a_n+（﹣1）ⁿa_n ，求数列{b_n}的前2n项和．

查看试题解析
20. 在△ABC中，角A，B，C所对的边分别为a，b，c，已知 $\frac{2 a + b}{c}$ = $\frac{\cos (A + C)}{\cos C}$

(1)、求角C的大小，

(2)、若c=2，求使△ABC面积最大时a，b的值．

查看试题解析
21. 某企业准备投入适当的广告费对产品进行促销，在一年内预计销售Q（万件）与广告费x（万元）之间的函数关系为Q= $\frac{3 x + 1}{x + 1}$ （x≥0）．已知生产此产品的年固定投入为3万元，每生产1万元此产品仍需再投入32万元，若每件销售价为“平均每件生产成本的150%”与“年平均每件所占广告费的50%”之和．

(1)、试将年利润W（万元）表示为年广告费x（万元）的函数；

(2)、当年广告费投入多少万元时，企业年利润最大？最大利润为多少？

查看试题解析
22. 已知函数f（x）满足f（x+y）=f（x）•f（y），且f（1）= $\frac{1}{2}$ ．

(1)、当n∈N^*时，求f（n）的表达式；

(2)、设a_n=n•f（n），n∈N^* ，求证a₁+a₂+a₃+…+a_n＜2；

(3)、设b_n=（9﹣n） $\frac{f (n + 1)}{f (n)}$ ，n∈N^* ， S_n为b_n的前n项和，当S_n最大时，求n的值．

查看试题解析