2016-2017学年重庆市江津区四校联考八年级上学期期中数学试卷
试卷更新日期：2016-12-13 类型：期中考试
一、选择题
-
1. 若一个三角形的两边长分别是3和4，则第三边的长可能是（ ）A、1 B、2 C、7 D、82. 下列图形中，不是轴对称图形的是（ ）A、
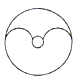B、
C、
D、
3. 一个多边形的内角和是1260°，这个多边形的边数是（ ）A、6 B、7 C、8 D、94. 如图，△ABE≌△ACF．若AB=5，AE=2，BE=4，则CF的长度是（ ）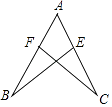
A、4 B、3 C、5 D、65. 如图，王师傅用4根木条钉成一个四边形木架，要使这个木架不变形，他至少要再钉上木条的根数是（ ）
A、0 B、1 C、2 D、36. 如图所示，某同学把一块三角形的玻璃不小心打碎成了三块，现在要到玻璃店去配一块完全一样的玻璃，那么最省事的办法是带（ ）去．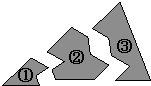
A、① B、② C、③ D、①和②7. 等腰三角形的一个角是80°，则它顶角的度数是（ ）A、80° B、80°或20° C、80°或50° D、20°8. 如图，将含30°角的三角板的直角顶点放在直尺的一边上，若∠1=40°，则∠2的度数为（ ）
A、90° B、80° C、75° D、70°9. 如图：△ABC中，AC=BC，∠C=90°，AD平分∠CAB交BC于D，DE⊥AB于E，且AC=6cm，则DE+BD等于（ ）
A、5cm B、4cm C、6cm D、7cm10. 如图，△ABC中，BD是∠ABC的角平分线，DE∥BC，交AB于E，∠A=60°，∠BDC=95°，则∠BED的度数是（ ）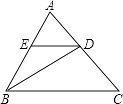
A、35° B、70° C、110° D、130°11. 在等腰三角形ABC中，AB=AC，一边上的中线BD将这个三角形的周长分为15和12两部分，则这个等腰三角形的底边长为（ ）A、7 B、7或11 C、11 D、7或1012. 如图，在△ABC中，AD是∠A的外角平分线，P是AD上异于A的任意一点，设PB=m，PC=n，AB=c，AC=b，则（m+n）与（b+c）的大小关系是（ ）
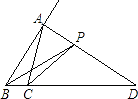A、m+n＞b+c B、m+n＜b+c C、m+n=b+c D、无法确定二、填空题
-
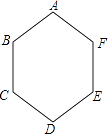
13. 如图，正六边形ABCDEF的每一个外角的度数是度．
14. 已知等腰三角形的两条边长分别为2和5，则它的周长为 ．15. 已知M（a，3）和N（4，b）关于y轴对称，则a+b的值为 ．16. 如图，AB=AC，若使△ABE≌△ACF，则还需要添加的条件是 ． （只要写出一个答案）．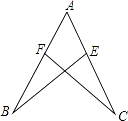
17. 如图，五边形ABCDE中，AB∥CD，∠1，∠2，∠3分别是∠BAE，∠AED，∠EDC的外角，则∠1+∠2+∠3= ．
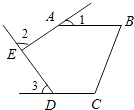18. 如图，在△ABC中，AB=AC，∠BAC=64°，∠BAC的平分线与AB的垂直平分线交于点O，将∠C沿EF（E在BC上，F在AC上）折叠，点C与点O恰好重合，则∠OEC为度．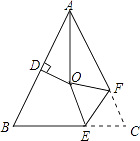
三、解答题
-
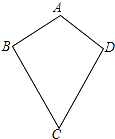
19. 如图，AB=AD，BC=DC，求证：∠ABC=∠ADC．
20. 如图，在△ABF与△CDE中，AB=CD，BF=DE，点A，E，F，C在同一条直线上，AE=CF，求证：AB∥CD．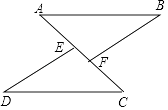
21. 如图，在直角坐标系中，△ABC各顶点的横、纵坐标都是整数，直线m上各点的横坐标都为﹣1．
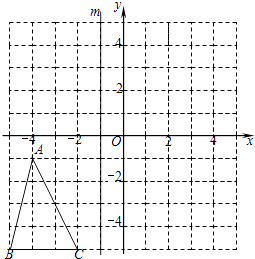(1)、①作出△ABC关于直线m的对称图形△A1B1C1；②作出△ABC关于x轴对称的图形△A2B2C2；
(2)、写出△A2B2C2的各顶点的坐标．22. 如图，已知在△ABC中，∠C=∠ABC=2∠A，BD是AC边上的高，求∠DBC的度数．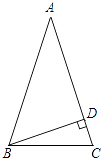
23. 已知，如图，DE⊥AC，BF⊥AC，AD=CB，DE=BF，求证：AB∥DC．
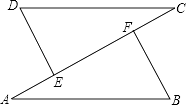24. 如图，在△ABC与△DCB中，AC与BD交于点E，且∠A=∠D，AB=DC．
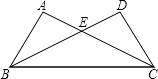(1)、求证：△ABE≌△DCE；(2)、当∠AEB=70°时，求∠EBC的度数．25. 如图，已知∠MAN=120°，AC平分∠MAN．B，D分别在射线AN，AM上．
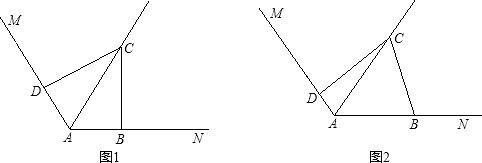(1)、在图（1）中，当∠ABC=∠ADC=90°时，求证：AD+AB=AC．(2)、若把（1）中的条件“∠ABC=∠ADC=90°”改为∠ABC+∠ADC=180°，其他条件不变，如图（2）所示．则（1）中的结论是否仍然成立？若成立，请给出证明；若不成立，请说明理由．26. 解答(1)、如图（1），已知：在△ABC中，∠BAC=90°，AB=AC，直线m经过点A，BD⊥直线m，CE⊥直线m，垂足分别为点D、E．证明：DE=BD+CE．
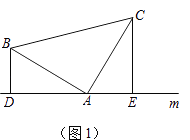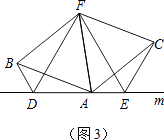
(2)、如图（2），将（1）中的条件改为：在△ABC中，AB=AC，D、A、E三点都在直线m上，并且有∠BDA=∠AEC=∠BAC=α，其中α为任意锐角或钝角．请问结论DE=BD+CE是否成立？如成立，请你给出证明；若不成立，请说明理由．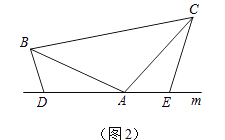
(3)、拓展与应用：如图（3），D、E是D、A、E三点所在直线m上的两动点（D、A、E三点互不重合），点F为∠BAC平分线上的一点，且△ABF和△ACF均为等边三角形，连接BD、CE，若∠BDA=∠AEC=∠BAC，试判断△DEF的形状．