2016-2017学年云南省保山市腾冲八中九年级上学期期中数学试卷
试卷更新日期:2016-12-13 类型:期中考试
一、认真填一填
-
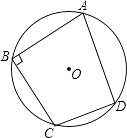
1. 分解因式:3x2﹣27= .2. 若关于x的函数y=kx2+2x﹣1与x轴仅有一个公共点,则实数k的值为 .3. 甲、乙玩猜数字游戏,游戏规则如下:有四个数字0、1、2、3,先由甲心中任选一个数字,记为m,再由乙猜甲刚才所选的数字,记为n.若m、n满足|m﹣n|≤1,则称甲、乙两人“心有灵犀”,则甲、乙两人“心有灵犀”的概率是 .4. 如图,点A,B,C,D都在⊙O上,∠ABC=90°,AD=3,CD=2,则⊙O的直径的长是
 5. 如图为二次函数y=ax2+bx+c的图象,在下列说法中:
5. 如图为二次函数y=ax2+bx+c的图象,在下列说法中:①ac<0;
②方程ax2+bx+c=0的根是x1=﹣1,x2=3;
③a+b+c>0;
④当x>1时,y随着x的增大而增大.
正确的说法有 . (请写出所有正确的序号)
 6. 如图,在平面直角坐标系xOy中,已知直线l:y=﹣x﹣1,双曲线y= ,在l上取一点A1 , 过A1作x轴的垂线交双曲线于点B1 , 过B1作y轴的垂线交l于点A2 , 请继续操作并探究:过A2作x轴的垂线交双曲线于点B2 , 过B2作y轴的垂线交l于点A3 , …,这样依次得到l上的点A1 , A2 , A3 , …,An , …记点An的横坐标为an , 若a1=2,则a2= , a2013=;若要将上述操作无限次地进行下去,则a1不可能取的值是 .
6. 如图,在平面直角坐标系xOy中,已知直线l:y=﹣x﹣1,双曲线y= ,在l上取一点A1 , 过A1作x轴的垂线交双曲线于点B1 , 过B1作y轴的垂线交l于点A2 , 请继续操作并探究:过A2作x轴的垂线交双曲线于点B2 , 过B2作y轴的垂线交l于点A3 , …,这样依次得到l上的点A1 , A2 , A3 , …,An , …记点An的横坐标为an , 若a1=2,则a2= , a2013=;若要将上述操作无限次地进行下去,则a1不可能取的值是 .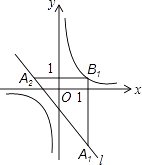
二、仔细选一选
-
7. ﹣7的倒数是( )A、﹣ B、7 C、 D、﹣78. 一年之中地球与太阳之间的距离随时间而变化,1个天文单位是地球与太阳之间平均距离,即1.4960亿千米,用科学记数法表示1个天文单位应是( )A、1.4960×千米 B、14.960×千米 C、1.4960×千米 D、0.14960×千米9. 分式方程 = 的解为( )A、x=﹣1 B、x=2 C、x=4 D、x=310. 如图,身高为1.5米的某学生想测量一棵大树的高度,她沿着树影BA由B向A走去当走到C点时,她的影子顶端正好与树的影子顶端重合,测得BC=3米,CA=1米,则树的高度为( )
 A、4.5米 B、6米 C、3米 D、4米11. 如图,在△ABC中,AB=12cm,BC=6cm,∠ABC=30°,把△ABC以点B为中心按逆时针方向旋转,使点C旋转到AB边的延长线上的C′处,那么AC边扫过的图形(图中阴影部分)的面积是( )cm2 . (结果保留π)
A、4.5米 B、6米 C、3米 D、4米11. 如图,在△ABC中,AB=12cm,BC=6cm,∠ABC=30°,把△ABC以点B为中心按逆时针方向旋转,使点C旋转到AB边的延长线上的C′处,那么AC边扫过的图形(图中阴影部分)的面积是( )cm2 . (结果保留π)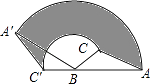 A、15π B、60π C、45π D、75π12. 为了帮助本市一名患“白血病”的高中生,某班15名同学积极捐款,他们捐款数额如下表:
A、15π B、60π C、45π D、75π12. 为了帮助本市一名患“白血病”的高中生,某班15名同学积极捐款,他们捐款数额如下表:捐款的数额(单位:元)
5
10
20
50
100
人数(单位:个)
2
4
5
3
1
关于这15名学生所捐款的数额,下列说法正确的是( )
A、众数是100 B、平均数是30 C、极差是20 D、中位数是2013. 反比例函数y=(k为常数)的图象位于( )A、第一、二象限 B、第一、三象限 C、第二、四象限 D、第三、四象限14. 如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,以点C为圆心,CA为半径的圆与AB交于点D,则AD的长为( )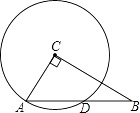 A、 B、 C、 D、
A、 B、 C、 D、三、全面答一答
-
15. 计算:|﹣3|﹣ ﹣(2016﹣π)+( )﹣1 .16. 解不等式组 ,并将解集在数轴上表示出来.
 17. 如图,点D,E在△ABC的边BC上,AB=AC,BD=CE.求证:AD=AE.
17. 如图,点D,E在△ABC的边BC上,AB=AC,BD=CE.求证:AD=AE.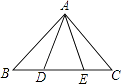 18. 青少年“心理健康”问题越来越引起社会的关注,某中学为了了解学校600名学生的心理健康状况,举行了一次“心理健康”知识测试,并随即抽取了部分学生的成绩(得分取正整数,满分为100分)作为样本,绘制了下面未完成的频率分布表和频率分布直方图.请回答下列问题:
18. 青少年“心理健康”问题越来越引起社会的关注,某中学为了了解学校600名学生的心理健康状况,举行了一次“心理健康”知识测试,并随即抽取了部分学生的成绩(得分取正整数,满分为100分)作为样本,绘制了下面未完成的频率分布表和频率分布直方图.请回答下列问题:分组
频数
频率
50.5~60.5
4
0.08
60.5~70.5
14
0.28
70.5~80.5
16
80.5~90.5
90.5~100.5
10
0.20
合计
1.00
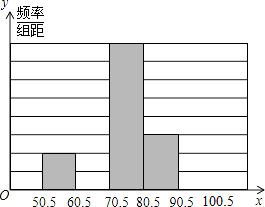 (1)、填写频率分布表中的空格,并补全频率分布直方图;(2)、若成绩在70分以上(不含70分)为心理健康状况良好,同时,若心理健康状况良好的人数占总人数的70%以上,就表示该校学生的心理健康状况正常,否则就需要加强心里辅导.请根据上述数据分析该校学生是否需要加强心里辅导,并说明理由.19. 小昆和小明玩摸牌游戏,游戏规则如下:有3张背面完全相同,牌面标有数字1、2、3的纸牌,将纸牌洗匀后背面朝上放在桌面上,随机抽出一张,记下牌面数字,放回后洗匀再随机抽出一张.
(1)、填写频率分布表中的空格,并补全频率分布直方图;(2)、若成绩在70分以上(不含70分)为心理健康状况良好,同时,若心理健康状况良好的人数占总人数的70%以上,就表示该校学生的心理健康状况正常,否则就需要加强心里辅导.请根据上述数据分析该校学生是否需要加强心里辅导,并说明理由.19. 小昆和小明玩摸牌游戏,游戏规则如下:有3张背面完全相同,牌面标有数字1、2、3的纸牌,将纸牌洗匀后背面朝上放在桌面上,随机抽出一张,记下牌面数字,放回后洗匀再随机抽出一张. (1)、请用画树形图或列表的方法(只选其中一种),表示出两次抽出的纸牌数字可能出现的所有结果;(2)、若规定:两次抽出的纸牌数字之和为奇数,则小昆获胜,两次抽出的纸牌数字之和为偶数,则小明获胜,这个游戏公平吗?为什么?20. 一辆客车从甲地开往乙地,一辆出租车从乙地开往甲地,两车同时出发,设客车离甲地的距离为y1千米,出租车离甲地的距离为y2千米,两车行驶的时间为x小时,y1、y2关于x的函数图象如图所示:
(1)、请用画树形图或列表的方法(只选其中一种),表示出两次抽出的纸牌数字可能出现的所有结果;(2)、若规定:两次抽出的纸牌数字之和为奇数,则小昆获胜,两次抽出的纸牌数字之和为偶数,则小明获胜,这个游戏公平吗?为什么?20. 一辆客车从甲地开往乙地,一辆出租车从乙地开往甲地,两车同时出发,设客车离甲地的距离为y1千米,出租车离甲地的距离为y2千米,两车行驶的时间为x小时,y1、y2关于x的函数图象如图所示: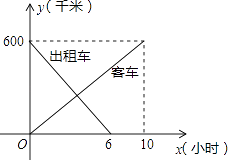 (1)、根据图象,直接写出y1、y2关于x的函数图象关系式;(2)、若两车之间的距离为S千米,请写出S关于x的函数关系式;(3)、甲、乙两地间有A,B两个加油站,相距200千米,若客车进入A加油站时,出租车恰好进入B加油站,求A加油站离甲地的距离.21. 如图1,△ABC中,CA=CB,点O在高CH上,OD⊥CA于点D,OE⊥CB于点E,以O为圆心,OD为半径作⊙O.
(1)、根据图象,直接写出y1、y2关于x的函数图象关系式;(2)、若两车之间的距离为S千米,请写出S关于x的函数关系式;(3)、甲、乙两地间有A,B两个加油站,相距200千米,若客车进入A加油站时,出租车恰好进入B加油站,求A加油站离甲地的距离.21. 如图1,△ABC中,CA=CB,点O在高CH上,OD⊥CA于点D,OE⊥CB于点E,以O为圆心,OD为半径作⊙O.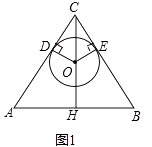 (1)、求证:⊙O与CB相切于点E;(2)、如图2,若⊙O 过点H,且AC=5,AB=6,连结EH,求△BHE的面积.
(1)、求证:⊙O与CB相切于点E;(2)、如图2,若⊙O 过点H,且AC=5,AB=6,连结EH,求△BHE的面积. 22. 如图,已知一条直线过点(0,4),且与抛物线y= x2交于A,B两点,其中点A的横坐标是﹣2.
22. 如图,已知一条直线过点(0,4),且与抛物线y= x2交于A,B两点,其中点A的横坐标是﹣2.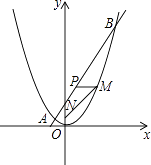 (1)、求这条直线的函数关系式及点B的坐标.(2)、在x轴上是否存在点C,使得△ABC是直角三角形?若存在,求出点C的坐标,若不存在,请说明理由.(3)、过线段AB上一点P,作PM∥x轴,交抛物线于点M,点M在第一象限,点N(0,1),当点M的横坐标为何值时,MN+3MP的长度最大?最大值是多少?
(1)、求这条直线的函数关系式及点B的坐标.(2)、在x轴上是否存在点C,使得△ABC是直角三角形?若存在,求出点C的坐标,若不存在,请说明理由.(3)、过线段AB上一点P,作PM∥x轴,交抛物线于点M,点M在第一象限,点N(0,1),当点M的横坐标为何值时,MN+3MP的长度最大?最大值是多少?