2017-2018学年数学浙教版八年级下册4.2.2平行四边形及其性质（课时2） 同步练习
试卷更新日期：2018-04-28 类型：同步测试
一、选择题
-
1. 下列命题中，真命题是（ ）A、对角线相等的四边形是矩形 B、对角线互相垂直平分的四边形是菱形 C、一组对边平行，另一组对边相等的四边形是平行四边形 D、一组邻边相等，并且有一个内角为直角的四边形是正方形
-
2.
如图，在△ABC中，BD、CE是△ABC的中线，BD与CE相交于点O，点F、G分别是BO、CO的中点，连接AO．若AO=6cm，BC=8cm，则四边形DEFG的周长是（ ）
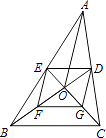A、14cm B、18cm C、24cm D、28cm -
3. 平行四边形的对角线一定具有的性质是（ ）A、相等 B、互相平分 C、互相垂直 D、互相垂直且相等
二、填空题
-
4. 四边形ABCD中，对角线AC、BD相交于点O，给出下列四个条件：
①AD∥BC；②AD=BC；③OA=OC；④OB=OD
从中任选两个条件，能使四边形ABCD为平行四边形的选法有种
-
5. 如图，△ACE是以▱ABCD的对角线AC为边的等边三角形，点C与点E关于x轴对称．若E点的坐标是（7，﹣3 ），则D点的坐标是 ．
-
6. 如图，平行四边形ABCD的对角线AC、BD交于一点O，AB=11，△OCD的周长为27，则AC+BD=
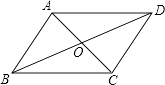
三、解答题
-
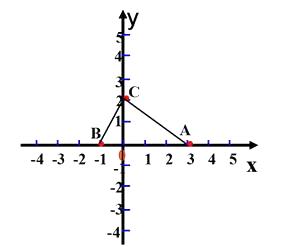
7. 已知点A（3，0）、B（-1，0）、C（0，2），以A、B、C为顶点画平行四边形，你能求出第四个顶点D吗？
-
8. 如果一条直线把一个平面图形的面积分成相等的两部分，我们把这条直线称为这个平面图形的一条面积等分线．(1)、平行四边形有条面积等分线；(2)、如图，四边形ABCD中，AB与CD不平行，AB≠CD，且S△ABC＜S△ACD ， 过点A画出四边形ABCD的面积等分线，并写出理由
-
9. 在
ABCD中，已知∠B=30°，将△ABC沿AC翻折至△AB′C，连结B′D.
(1)、如图1，若
，则∠ACB=°，BC=； (2)、如图2，
，BC=1，AB′与边CD相交于点E，求△AEC的面积； (3)、已知 ，当BC长为多少时，是△AB′D直角三角形？
