2017-2018学年数学浙教版八年级下册4.4.1平行四边形的判定定理(课时1) 同步练习
试卷更新日期:2018-04-28 类型:同步测试
一、选择题
-
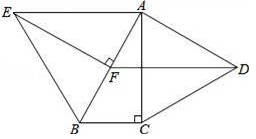
1. 如图,在▱ABCD中,AB=4,∠BAD的平分线与BC的延长线相交于点E,与DC交于点F,且点F为边DC的中点,DG⊥AE,垂足为G,若DG=1,则AE的长为( )
 A、2 B、4 C、4 D、82. 已知四边形ABCD,有下列条件:①AB∥CD;②BC∥AD;③AB=CD;④BC=AD;⑤∠A=∠C;⑥∠B=∠D. 任取其中两个,可以得出“四边形ABCD是平行四边形”这一结论的情况有( )A、4种 B、9种 C、13种 D、15种3. 已知四边形ABCD的四条边长分别为a,b,c,d,其中a,b为对边,且a2+b2+c2+d2=2ab+2cd,则此四边形一定是( )A、任意四边形 B、对角线相等的四边形 C、对角线互相垂直且相等的四边形 D、平行四边形
A、2 B、4 C、4 D、82. 已知四边形ABCD,有下列条件:①AB∥CD;②BC∥AD;③AB=CD;④BC=AD;⑤∠A=∠C;⑥∠B=∠D. 任取其中两个,可以得出“四边形ABCD是平行四边形”这一结论的情况有( )A、4种 B、9种 C、13种 D、15种3. 已知四边形ABCD的四条边长分别为a,b,c,d,其中a,b为对边,且a2+b2+c2+d2=2ab+2cd,则此四边形一定是( )A、任意四边形 B、对角线相等的四边形 C、对角线互相垂直且相等的四边形 D、平行四边形二、填空题
-
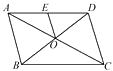
4. 如图,▱ABCD的对角线AC,BD相交于点O,点E是AD的中点,△BCD的周长为8 cm,则△DEO的周长是 cm.
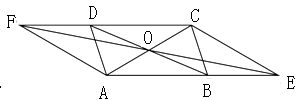
 5. 如图,▱ABCD与▱DCFE的周长相等,且∠BAD=60°,∠F=110°,则∠DAE的度数为 .
5. 如图,▱ABCD与▱DCFE的周长相等,且∠BAD=60°,∠F=110°,则∠DAE的度数为 .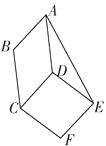 6. 如图,在▱ABCD中,DE平分∠ADC,AD=6,BE=2,则▱ABCD的周长是.
6. 如图,在▱ABCD中,DE平分∠ADC,AD=6,BE=2,则▱ABCD的周长是.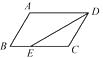
三、解答题
-
7. 如图,在▱ABCD中,点E、F是对角线AC上两点,且AE=CF.
求证:∠EBF=∠FDE.
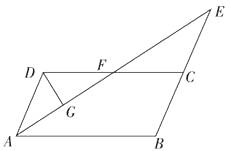
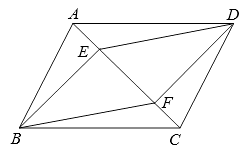 8. 如图,在▱ABCD中,E,F分别为AD,BC的中点,连结BE,AF交于点G,连结DF,EC交于点H.求证:四边形EGFH是平行四边形.
8. 如图,在▱ABCD中,E,F分别为AD,BC的中点,连结BE,AF交于点G,连结DF,EC交于点H.求证:四边形EGFH是平行四边形.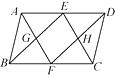 9. 如图,平行四边形ABCD的对角线相交于点O,直线EF经过点O,分别与AB,CD的延长线交于点E,F
9. 如图,平行四边形ABCD的对角线相交于点O,直线EF经过点O,分别与AB,CD的延长线交于点E,F求证:四边形AECF是平行四边形.