上海市浦东新区第一教育署2017-2018学年七年级下学期数学期中考试试卷(五四学制)
试卷更新日期:2018-04-28 类型:期中考试
一、选择题:
-
1. 在 ,1.01001000100001,2 ,3.1415,- , ,0, ,这些数中,无理数共有( )A、2个 B、3个 C、4个 D、5个2. 下列语句正确是( )A、无限小数是无理数 B、无理数是无限小数 C、实数分为正实数和负实数 D、两个无理数的和还是无理数3. 数轴上点A与点B之间的距离为m,且点A在点B的左侧,若点B所对应的数是- ,则点A所对应的数是( )
A、m+ B、m- C、–m+ D、–m-4. 下列图形中,∠1和∠2不是同位角的是( )A、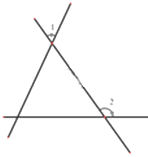 B、
B、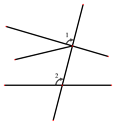 C、
C、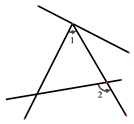 D、
D、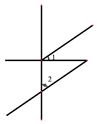 5. 下列说法正确的个数有( )
5. 下列说法正确的个数有( )⑴过一点有且只有一条直线与已知直线平行⑵一条直线有且只有一条垂线⑶不相交的两条直线叫做平行线⑷直线外一点到这条直线的垂线段叫做这点到这条直线的距离
A、0个 B、1个 C、2个 D、3个6. 已知OA⊥OC,如果∠AOC:∠AOB=3:2,那么∠BOC的大小为( )A、30° B、150° C、30°或150° D、90°二、填空题:
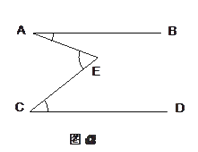
-
7. 计算: 的七次方根是.8. 若x2=5,则x=.
9. 比较大小-5 -4 (用“>”、“<”或“=”填空)10. 月球沿着一定的轨道围绕地球运动,某一时刻它与地球相距405 500千米,用科学记数法表示这个数并保留三个有效数字是千米.
11. 如图,图中,∠B的同旁内角除了∠A还有. 12. 把 表示成幂的形式是.13. 已知,直线AB和直线CD交与点O,∠BOD是它的邻补角的3倍,则直线AB与直线CD的夹角是度.
12. 把 表示成幂的形式是.13. 已知,直线AB和直线CD交与点O,∠BOD是它的邻补角的3倍,则直线AB与直线CD的夹角是度.
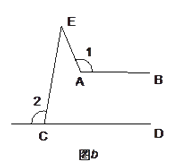
14. 化简( )2+ =.15. 如图,直线AB与CD相交于点O,∠AOE=90°,且∠EOD= ∠COE,∠BOD=°.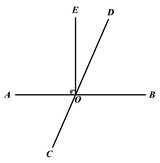 16. 如图,有一个长方形纸片,减去相邻的两个角,使∠ABC=90°,如果∠1=152°,那么∠2=°.
16. 如图,有一个长方形纸片,减去相邻的两个角,使∠ABC=90°,如果∠1=152°,那么∠2=°.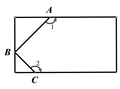 17. 如果一个角的两边分别与另一个角的两边平行,那么这两个角的大小关系是.
17. 如果一个角的两边分别与另一个角的两边平行,那么这两个角的大小关系是.
18. 如图,把一个长方形纸片沿EF折叠后,点D、C分别落在D′、C′的位置.若∠EFB=65°,则∠AED′的度数是.
三、简答题:
-
19. 计算:-3 - (6 - )20. 计算:21. 计算22. 计算23. 利用幂的运算性质进行计算:
24. 已知a的两个平方根x、 y为4x-3y-28=0的一组解,求4a的算术平方根.
四、解答题:
-
25. 按下列要求画图并填空:
 (1)、画图:
(1)、画图:① 过点A画AD⊥BC,垂足为D
② 过点C画CE⊥AB,垂足为E
③ 过点B画BF⊥AC,垂足为F
(2)、填空:① 点B、C两点的距离是线段的长度,AD的长度表示点A到直线的距离.
② 点B到直线AC的距离是线段的长度.
③点E到直线AB的距离是.
26. 如图,AE、BF、DC是直线,B在直线AC上,E在直线DF上,∠1=∠2,∠A=∠F.求证:∠C=∠D.

证明:因为∠1=∠2(已知),∠1=∠3
得∠2=∠3
所以AE//
得∠4=∠F
因为(已知)
得∠4=∠A
所以//
所以∠C=∠D