安徽省合肥市2017-2018学年七年级下学期数学期中考试试卷
试卷更新日期:2018-04-28 类型:期中考试
一、单选题
-
1. 下列各图中,∠1与∠2是对顶角的是( )A、
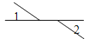 B、
B、 C、
C、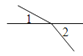 D、
D、 2. 的平方根是( )A、2 B、±2 C、 D、±3. 在下列所给出的坐标中,在第二象限的是( )A、(2,3) B、(2,-3) C、(-2,-3) D、(-2,3)4. 在实数
2. 的平方根是( )A、2 B、±2 C、 D、±3. 在下列所给出的坐标中,在第二象限的是( )A、(2,3) B、(2,-3) C、(-2,-3) D、(-2,3)4. 在实数 ,
, 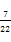 ,
, 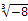 , 0,-1.414,
, 0,-1.414,  ,
,  ,0.1010010001中,无理数有( ) A、2个 B、3个 C、4个 D、5个5.
,0.1010010001中,无理数有( ) A、2个 B、3个 C、4个 D、5个5.如图,点E在BC的延长线上,下列条件中不能判定AB∥CD的是( )
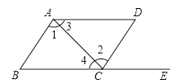 A、∠3=∠4 B、∠1=∠2 C、∠B=∠DCE D、∠D+∠DAB=180°6. 下列命题是假命题的是( )A、对顶角相等 B、两直线平行,同旁内角相等 C、平行于同一条直线的两直线平行 D、同位角相等,两直线平行7. 如图,表示
A、∠3=∠4 B、∠1=∠2 C、∠B=∠DCE D、∠D+∠DAB=180°6. 下列命题是假命题的是( )A、对顶角相等 B、两直线平行,同旁内角相等 C、平行于同一条直线的两直线平行 D、同位角相等,两直线平行7. 如图,表示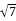 的点在数轴上表示时,应在哪两个字母之间( )
的点在数轴上表示时,应在哪两个字母之间( ) A、C与D B、A与B C、A与C D、B与C8. 点P位于x轴下方,y轴左侧,距离x轴4个单位长度,距离y轴2个单位长度,那么点P的坐标是( )A、(4,2) B、(-2,-4) C、(-4,-2) D、(2,4)9. 在平面直角坐标系中,线段CF是由线段AB平移得到的;点A(-1,4)的对应点为C(4,1);则点B(a,b)的对应点F的坐标为( )A、(a+3,b+5) B、(a+5,b+3) C、(a-5,b+3) D、(a+5,b-3)10. 如图所示,将含有30°角的三角板的直角顶点放在相互平行的两条直线其中一条上,若∠1=35°,则∠2的度数为( )
A、C与D B、A与B C、A与C D、B与C8. 点P位于x轴下方,y轴左侧,距离x轴4个单位长度,距离y轴2个单位长度,那么点P的坐标是( )A、(4,2) B、(-2,-4) C、(-4,-2) D、(2,4)9. 在平面直角坐标系中,线段CF是由线段AB平移得到的;点A(-1,4)的对应点为C(4,1);则点B(a,b)的对应点F的坐标为( )A、(a+3,b+5) B、(a+5,b+3) C、(a-5,b+3) D、(a+5,b-3)10. 如图所示,将含有30°角的三角板的直角顶点放在相互平行的两条直线其中一条上,若∠1=35°,则∠2的度数为( )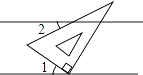 A、10° B、20° C、25° D、30°
A、10° B、20° C、25° D、30°二、填空题
-
11. 若整数x满足|x|≤3,则使为整数的x的值是(只需填一个).
12. 把5的平方根和立方根按从小到大的顺序排列为 .13. 如图所示,在平面直角坐标系中,一动点从原点O出发,按向上,向右,向下,向右的方向不断地移动,每移动一个单位,得到点A1(0,1),A2(1,1),A3(1,0),A4(2,0),…,那么点A4n+1(n为自然数)的坐标为(用n表示).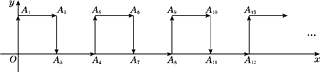
三、解答题
-
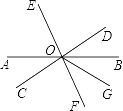
14. 如图所示,直线AB、CD、EF交于点O,OG平分∠BOF,且CD⊥EF,∠AOE=70°,求∠DOG的度数.
 15. 计算:
15. 计算:
(1)、 +(2)、| -2|-16. 求下列各式中x的值:
(1)、2x2=4;(2)、64x3 + 27=017. 如图,直线a∥b,点B在直线b上,且AB⊥BC,∠1=55°,求∠2的度数.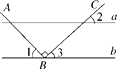 18. 完成下面的证明
18. 完成下面的证明如图,点E在直线DF上,点B在直线AC上,若∠AGB=∠EHF,∠C=∠D.
求证:∠A=∠F.
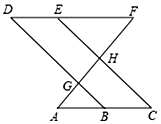
证明:∵∠AGB=∠EHF
∠AGB=(对顶角相等)
∴∠EHF=∠DGF
∴DB∥EC()
∴∠=∠DBA()
又∵∠C=∠D
∴∠DBA=∠D
∴DF∥()
∴∠A=∠F().
19. 已知5a+2的立方根是3,3a+b-1的算术平方根是4,c是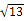 的整数部分. (1)、求a,b,c的值;(2)、求3a-b+c的平方根20. 如图,直线AB是某天然气公司的主输气管道,点C、D是在AB异侧的两个小区,现在主输气管道上寻找支管道连接点,向两个小区铺设管道。有以下两个方案:
的整数部分. (1)、求a,b,c的值;(2)、求3a-b+c的平方根20. 如图,直线AB是某天然气公司的主输气管道,点C、D是在AB异侧的两个小区,现在主输气管道上寻找支管道连接点,向两个小区铺设管道。有以下两个方案:方案一:只取一个连接点P,使得像两个小区铺设的支管道总长度最短,在图中标出点P的位置,保留画图痕迹;
方案二:取两个连接点M和N,使得点M到C小区铺设的支管道最短,使得点N到D小区铺设的管道最短. 在途中标出M、N的位置,保留画图痕迹;
设方案一中铺设的支管道总长度为L1 , 方案二中铺设的支管道总长度为L2 , 则L1与L2的大小关系为:L1L2(填“>”、“<”或“=”)理由是.
 21. 如图,这是某市部分简图,为了确定各建筑物的位置请完成以下步骤.
21. 如图,这是某市部分简图,为了确定各建筑物的位置请完成以下步骤.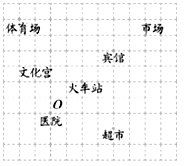 (1)、请你以火车站为原点建立平面直角坐标系;(2)、写出市场的坐标是;超市的坐标为;(3)、请将体育场为A、宾馆为C和火车站为B看作三点用线段连起来,得△ABC,然后将此三角形向下平移4个单位长度,画出平移后的△A1B1C1 , 并求出其面积.22. 如图,长方形OABC中,O为直角坐标系的原点,A、C两点的坐标分别为(6,0),(0,10),点B在第一象限内.
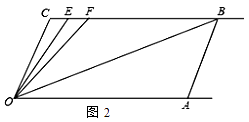
(1)、请你以火车站为原点建立平面直角坐标系;(2)、写出市场的坐标是;超市的坐标为;(3)、请将体育场为A、宾馆为C和火车站为B看作三点用线段连起来,得△ABC,然后将此三角形向下平移4个单位长度,画出平移后的△A1B1C1 , 并求出其面积.22. 如图,长方形OABC中,O为直角坐标系的原点,A、C两点的坐标分别为(6,0),(0,10),点B在第一象限内.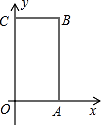 (1)、写出点B的坐标,并求长方形OABC的周长;(2)、若有过点C的直线CD把长方形OABC的周长分成3:5两部分,D为直线CD与长方形的边的交点,求点D的坐标.23. 如图1,已知射线CB∥OA,∠C=∠OAB,
(1)、写出点B的坐标,并求长方形OABC的周长;(2)、若有过点C的直线CD把长方形OABC的周长分成3:5两部分,D为直线CD与长方形的边的交点,求点D的坐标.23. 如图1,已知射线CB∥OA,∠C=∠OAB, (1)、求证:AB∥OC;(2)、如图2,E、F在CB上,且满足∠FOB=∠AOB,OE平分∠COF.
(1)、求证:AB∥OC;(2)、如图2,E、F在CB上,且满足∠FOB=∠AOB,OE平分∠COF.①当∠C=110°时,求∠EOB的度数.
②若平行移动AB,那么∠OBC :∠OFC的值是否随之发生变化?若变化,找出变
化规律;若不变,求出这个比值.