2017-2018学年数学浙教版九年级下册2.2 切线长定理 同步练习
试卷更新日期:2018-04-28 类型:同步测试
一、基础训练
-
1. 下列说法正确的是( )A、过任意一点总可以作圆的两条切线 B、圆的切线长就是圆的切线的长度 C、过圆外一点所画的圆的两条切线长相等 D、过圆外一点所画的圆的切线长一定大于圆的半径2. 如图,PA,PB是☉O的切线,A,B是切点,且∠APB=40°,下列结论不正确的是( )
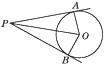 A、PA=PB B、∠APO=20° C、∠OBP=70° D、∠AOP=70°3. 如图,从圆O外一点P引圆O的两条切线PA,PB,切点分别为A,B.如果∠APB=60°,PA=8,那么弦AB的长是( )
A、PA=PB B、∠APO=20° C、∠OBP=70° D、∠AOP=70°3. 如图,从圆O外一点P引圆O的两条切线PA,PB,切点分别为A,B.如果∠APB=60°,PA=8,那么弦AB的长是( )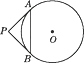 A、4 B、8 C、 D、4. 如图,PA,PB是☉O的切线,A,B为切点,AC是☉O的直径,已知∠BAC=15°,则∠P的度数为( )
A、4 B、8 C、 D、4. 如图,PA,PB是☉O的切线,A,B为切点,AC是☉O的直径,已知∠BAC=15°,则∠P的度数为( )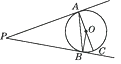 A、30° B、35° C、40° D、45°5. 如图,PA切☉O于A,PB切☉O于B,连结OP,AB.下列结论不一定正确的是( )
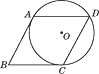
A、30° B、35° C、40° D、45°5. 如图,PA切☉O于A,PB切☉O于B,连结OP,AB.下列结论不一定正确的是( )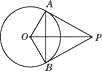 A、PA=PB B、OP垂直平分AB C、∠OPA=∠OPB D、PA=AB6. 如图,圆和四边形ABCD的四条边都相切,且AB=16,CD=10,则四边形ABCD的周长为( )
A、PA=PB B、OP垂直平分AB C、∠OPA=∠OPB D、PA=AB6. 如图,圆和四边形ABCD的四条边都相切,且AB=16,CD=10,则四边形ABCD的周长为( )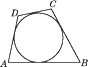 A、50 B、52 C、54 D、567. 如图,AC是☉O的直径,∠ACB=60°,连结AB,过A,B两点分别作☉O的切线,两切线交于点P,若☉O的半径为1,则△PAB的周长为.
A、50 B、52 C、54 D、567. 如图,AC是☉O的直径,∠ACB=60°,连结AB,过A,B两点分别作☉O的切线,两切线交于点P,若☉O的半径为1,则△PAB的周长为. 8. 如图,PA,PB是☉O的切线,A,B分别为切点,AC是☉O的直径,∠P=40°,则∠BAC=.
8. 如图,PA,PB是☉O的切线,A,B分别为切点,AC是☉O的直径,∠P=40°,则∠BAC=.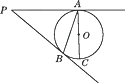 9. 既有外接圆,又有内切圆的平行四边形是( )
9. 既有外接圆,又有内切圆的平行四边形是( )
A、矩形 B、菱形 C、正方形 D、平行四边形10. 如图,☉O与四边形ABCD的四边都相切.若∠AOB=70°,求∠COD的度数.
二、提升训练
-
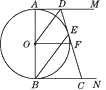
11. 如图,以Rt△ABC的直角边AB为直径作☉O,与斜边AC交于点D,过点D作☉O的切线交BC边于点E.求证:EB=EC=ED
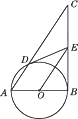 12. 如图,PA,PB是☉O的切线,切点分别为A,B,BC为☉O的直径,连结AB,AC,OP.
12. 如图,PA,PB是☉O的切线,切点分别为A,B,BC为☉O的直径,连结AB,AC,OP.
求证:
(1)、∠APB=2∠ABC(2)、AC∥OP.13. 综合题
(1)、如图,四边形ABCD是☉O的外切四边形,切点分别为E,F,G,H,说明AB+CD与BC+AD的大小关系. (2)、如图,四边形ABCD的三边切☉O于F,G,H,说明AB+CD与BC+AD的大小关系.
(2)、如图,四边形ABCD的三边切☉O于F,G,H,说明AB+CD与BC+AD的大小关系. (3)、如图,四边形ABCD的三边切☉O于F,G,H,说明AB+CD与BC+AD的大小关系.
(3)、如图,四边形ABCD的三边切☉O于F,G,H,说明AB+CD与BC+AD的大小关系.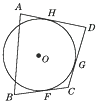 14. 如图,PA,PB分别切☉O于A,B,连结PO,AB,相交于点D,C是☉O上一点,∠C=60°.
14. 如图,PA,PB分别切☉O于A,B,连结PO,AB,相交于点D,C是☉O上一点,∠C=60°.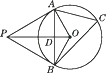 (1)、求∠APB的大小;(2)、若PO=20 cm,求△AOB的面积.
(1)、求∠APB的大小;(2)、若PO=20 cm,求△AOB的面积.