2017-2018学年数学浙教版九年级下册2.1.2 直线与圆的位置关系—切线的判定和性质 同步练习
试卷更新日期：2018-04-28 类型：同步测试
一、基础训练
-
1. 下列说法正确的是（ ）A、与圆有公共点的直线是圆的切线 B、圆心到直线的距离等于圆的半径的直线是圆的切线 C、垂直于圆的半径的直线是圆的切线 D、经过圆的半径外端的直线是圆的切线2. 如图，点A，B，D在☉O上，∠A=25°，OD的延长线交直线BC于点C，当∠OCB=（ ）时，直线BC与☉O相切.
A、25° B、40° C、50° D、60°3. 如图，△ABC是☉O的内接三角形，下列选项中，能使过点A的直线EF与☉O相切于点A的条件是（ ）
A、∠EAB=∠C B、∠B=90° C、EF⊥AC D、AC是☉O的直径4. 如图，在平面直角坐标系中，☉O的半径为1，则直线y=x- 与☉O的位置关系是（ ）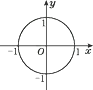
A、相离 B、相切 C、相交 D、以上三种情况都有可能5. 如图，P是☉O外一点，PA是☉O的切线，PO=26 cm，PA=24 cm，则☉O的周长为（ ）
A、18π cm B、16π cm C、20π cm D、24π cm6. 下列说法中，错误的是（ ）A、垂直于弦的直径平分这条弦 B、弦的垂直平分线过圆心 C、垂直于圆的切线的直线必过圆心 D、经过圆心且垂直于切线的直线必经过切点7. 如图，在等腰直角三角形ABC中，AB=AC=4，点O为BC的中点，以O为圆心作半圆O交BC于点M，N，半圆O与AB，AC相切，切点分别为D，E，则半圆O的半径和∠MND的度数分别为（ ）
A、2；22.5° B、3；30° C、3；22.5° D、2；30°8. 如图，O是正方形ABCD的对角线BD上一点，☉O与边AB，BC都相切，点E，F分别在边AD，DC上.现将△DEF沿着EF折叠，折痕EF与☉O相切，此时点D恰好落在圆心O处.若DE=2，则正方形ABCD的边长是（ ）
A、3 B、4 C、2+ D、29. 如图，以等边三角形ABC的BC边为直径画半圆，分别交AB，AC于点E，D，DF是半圆O的切线，过点F作BC的垂线交BC于点G.若AF的长为2，则FG的长为（ ）
A、4 B、3 C、6 D、210. 如图，点O为∠MPN的平分线上一点，以点O为圆心的☉O与PN相切于点A.求证：PM为☉O的切线.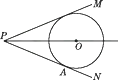
二、提升训练
-
11. 如图，AB是☉O的直径，BC⊥AB，连结OC，弦AD∥OC，直线CD交BA的延长线于点E.
(1)、求证：直线CD是☉O的切线；(2)、若DE=2BC，求AD∶OC的值.12. 如图，在Rt△ABC中，∠ABC=90°，∠BAC的平分线交BC于D，以D为圆心，DB为半径作☉D.求证：AC与☉D相切.
13. 如图，△ABC是边长为4的等边三角形，点O在边AB上，☉O过点B且分别与边AB，BC相交于点D，E，EF⊥AC，垂足为F.
(1)、求证：直线EF是☉O的切线；(2)、当直线DF与☉O相切时，求☉O的半径.14. 如图，P是☉O外一点，PO交☉O于点C，OC=CP=2，弦AB⊥OC，劣弧AB的度数为120°，连结PB，BC.
(1)、求BC的长；(2)、求证：PB是☉O的切线.15. 如图，AB是☉O的直径，OD垂直弦AC于点E，且交☉O于点D，F是BA的延长线上一点，若∠CDB=∠BFD，求证：FD是☉O的切线.
16. 已知AB是半圆O的直径，点C是半圆O上的动点，点D是线段AB的延长线上的动点，在运动过程中，保持CD=OA.
(1)、当直线CD与半圆O相切时(如图①)，求∠ODC的度数.(2)、当直线CD与半圆O相交时(如图②)，设另一交点为E，连结AE，若AE∥OC，①线段AE与OD的大小有什么关系?为什么?
②求∠ODC的度数.
