2017-2018学年数学浙教版九年级下册2.1.1 直线与圆的位置关系 同步练习

试卷更新日期：2018-04-28 类型：同步测试

进入 出卷网 下载

一、基础训练

  • 1. 若直线l与☉O有公共点，则直线l与☉O的位置关系可能是（ ）
    A、相交或相切 B、相交或相离 C、相切或相离 D、无法确定

    查看试题解析

  • 2. 已知☉O的半径r=2 cm，☉O的圆心到直线l的距离d= 2 cm，则直线l与☉O的位置关系是（ ）
    A、相离 B、相交 C、相切 D、无法确定

    查看试题解析

  • 3. 如图，☉O的圆心O到直线l的距离为3 cm，☉O的半径为1 cm，将直线l向右(垂直于l的方向)平移，使l与☉O相切，则平移的距离为（ ）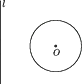


    A、1 cm B、2 cm C、4 cm D、2 cm或4 cm

    查看试题解析

  • 4. 在平面直角坐标系中，以点(-3，4)为圆心，4为半径的圆（ ）
    A、与x轴相交，与y轴相切 B、与x轴相离，与y轴相交 C、与x轴相切，与y轴相离 D、与x轴相切，与y轴相交

    查看试题解析

  • 5. 如图，在Rt△ABC中，∠C=90°，∠B=30°，BC=4 cm，以点C为圆心，以2 cm为半径作圆，则☉C与AB的位置关系是（ ）

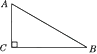    A、相离 B、相切 C、相交 D、相切或相交

    查看试题解析

  • 6. 已知直线l与半径为r的☉O相交，且点O到直线l的距离为6，则r的取值范围是（ ）
    A、r<6 B、r=6 C、r>6 D、r≥6

    查看试题解析

  • 7. 如图，以点O为圆心的两个圆，半径分别为5和3，若大圆的弦AB与小圆相交，则弦AB的长度的取值范围是（ ）

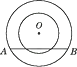    A、8≤AB≤10 B、AB≥8 C、8<AB≤10 D、8<AB<10

    查看试题解析

  • 8. 设☉O的半径为R，圆心O到直线l的距离为d，若d，R是方程x2-6x+m=0的两根，则直线l与☉O相切时，m的值为.

    查看试题解析

  • 9. 在直角坐标系中，☉M的圆心坐标是(m，0)，半径是2，如果☉M与y轴相切，那么m=；如果☉M与y轴相交，那么m的取值范围是.

    查看试题解析

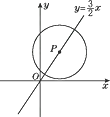
  • 10. 如图，在平面直角坐标系第一象限内有一矩形OABC，B(4，2)，现有一圆同时和这个矩形的三边都相切，则此圆的圆心P的坐标为.

    查看试题解析

  • 11. 已知☉O的半径为5，点P在直线l上，且OP=5，则直线l与☉O的位置关系是（ ）
    A、相切 B、相交 C、相离 D、相切或相交

    查看试题解析

二、提升训练

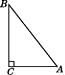
  • 12. 如图，在Rt△ABC中，∠ACB=90°，AB=5 cm，AC=3 cm.以点C为圆心，r为半径的圆和直线AB有何位置关系?

    查看试题解析

  • 13. 已知∠MAN=30°，O为边AN上一点，以O为圆心，2为半径作☉O，交AN于D，E两点，设AD=x.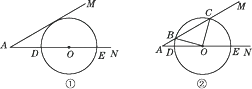

    (1)、如图①，当x取何值时，☉O与AM相切?
    (2)、如图②，当x取何值时，☉O与AM相交于B，C两点，且∠BOC=90°?

    查看试题解析

  • 14. 已知☉O的半径r=3，设圆心O到一条直线的距离为d，圆上到这条直线的距离为2的点的个数为m，给出下列命题：①若d>5，则m=0；②若d=5，则m=1；③若1<d<5，则m=3；④若d=1，则m=2；⑤若d<1，则m=4.

    其中正确命题的个数是（ ）

    A、1 B、3 C、4 D、5

    查看试题解析

  • 15. 如图，P为正比例函数y= 32 x图象上的一个动点，☉P的半径为3，设点P的坐标为(x，y).

    (1)、求☉P与直线x=2相切时点P的坐标；
    (2)、请直接写出☉P与直线x=2相交、相离时，x的取值范围.

    查看试题解析