贵州省遵义市2018届数学中考模拟试卷(3)
试卷更新日期:2018-04-28 类型:中考模拟
一、选择题
-
1. -2017的绝对值是( )
A、2017 B、-2017 C、 D、-2. 下列图案中,既是轴对称图形又是中心对称图形的是( )
A、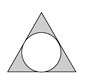 B、
B、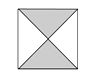 C、
C、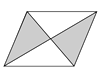 D、
D、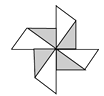 3. 下列各式计算正确的是( )A、x2+x3=x5 B、(mn3)2=mn6 C、(a-b)2=a2-b2 D、p6÷p2=p4(p≠0)4. 如图所示,已知AB∥CD,∠1=60°,则∠2的度数是( )
3. 下列各式计算正确的是( )A、x2+x3=x5 B、(mn3)2=mn6 C、(a-b)2=a2-b2 D、p6÷p2=p4(p≠0)4. 如图所示,已知AB∥CD,∠1=60°,则∠2的度数是( )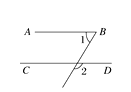 A、30° B、60° C、120° D、150°5. 在今年遵义市中考体育考试中,某小组7名考生“一分钟跳绳”的成绩(单位:个/分)分别为:178,183,182,181,183,183,182.这组数据的众数和中位数分别为( )
A、30° B、60° C、120° D、150°5. 在今年遵义市中考体育考试中,某小组7名考生“一分钟跳绳”的成绩(单位:个/分)分别为:178,183,182,181,183,183,182.这组数据的众数和中位数分别为( )
A、183,182 B、182,183 C、182,182 D、183,1836. 不等式组 的解集在数轴上表示正确的是( )
A、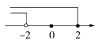 B、
B、 C、
C、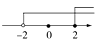 D、
D、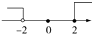 7. 已知点A(x1 , y1)、B(x2 , y2)是直线y=- x+2上不同的两点,且x1<x2 , 若m=(x1-x2)(y1-y2)则( )
7. 已知点A(x1 , y1)、B(x2 , y2)是直线y=- x+2上不同的两点,且x1<x2 , 若m=(x1-x2)(y1-y2)则( )
A、m=0 B、m<0 C、m>0 D、不能比较8. 如图,△DEF是由△ABC经过位似变换得到的,点O是位似中心,D,E,F分别是OA,OB,OC的中点,则△DEF与△ABC的面积比是( )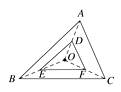 A、1∶2 B、1∶4 C、1∶5 D、1∶69. 函数y= + 中自变量x的取值范围是( )A、x≤2 B、x≠-1 C、x≤2且x≠0 D、x≤2且x≠-110. 如图所示,将矩形ABCD绕点A顺时针旋转到矩形AB′C′D′的位置,旋转角为α(0°<α<90°).若∠1=110°,则旋转角α的度数为( )
A、1∶2 B、1∶4 C、1∶5 D、1∶69. 函数y= + 中自变量x的取值范围是( )A、x≤2 B、x≠-1 C、x≤2且x≠0 D、x≤2且x≠-110. 如图所示,将矩形ABCD绕点A顺时针旋转到矩形AB′C′D′的位置,旋转角为α(0°<α<90°).若∠1=110°,则旋转角α的度数为( )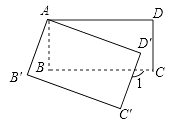 A、10° B、15° C、20° D、25°11. 如图,正方形ABCD边长为4,以BC为直径的半圆O交对角线BD于点E.则阴影部分面积为( )
A、10° B、15° C、20° D、25°11. 如图,正方形ABCD边长为4,以BC为直径的半圆O交对角线BD于点E.则阴影部分面积为( )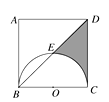 A、6-π B、2 -π C、 π D、π12. 如图,在平行四边形ABCD中,AB=6,AD=9,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE于点G,BG=4 ,则△EFC的周长为( )
A、6-π B、2 -π C、 π D、π12. 如图,在平行四边形ABCD中,AB=6,AD=9,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE于点G,BG=4 ,则△EFC的周长为( ) A、11 B、10 C、9 D、8
A、11 B、10 C、9 D、8二、填空题
-
13. 分解因式:ab2-4ab+4a=.14. 计算: -6 =15. 如图所示,王华晚上由路灯A下的B处走到C处时,测得影子CD的长为1米,继续往前走3米到达E处时,测得影子EF的长为2米,已知王华的身高是1.5米,那么路灯A的高度AB等于米.
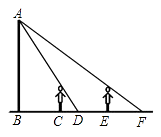
16. 如图,在圆O中,AB、AC为互相垂直且相等的两条弦,OD⊥AB,OE⊥AC,垂足分别为D、E,若AC=2cm,则圆O的半径为cm. 17. 如图,点A在双曲线y= 上,点B在双曲线y= (k≠0)上,AB∥x轴,分别过点A、B向x轴作垂线,垂足分别为D、C,若矩形ABCD的面积是12,则k的值为.
17. 如图,点A在双曲线y= 上,点B在双曲线y= (k≠0)上,AB∥x轴,分别过点A、B向x轴作垂线,垂足分别为D、C,若矩形ABCD的面积是12,则k的值为.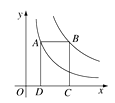 18. 如图,在正方形ABCD中,边长为2的等边三角形AEF的顶点E,F分别在BC和CD上,下列结论:①CE=CF;②∠AEB=75°;③BE+DF=EF;④S正方形ABCD=2+ .其中正确的序号是_.(把你认为正确的都填上)
18. 如图,在正方形ABCD中,边长为2的等边三角形AEF的顶点E,F分别在BC和CD上,下列结论:①CE=CF;②∠AEB=75°;③BE+DF=EF;④S正方形ABCD=2+ .其中正确的序号是_.(把你认为正确的都填上)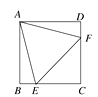
三、解答题
-
19. 计算:( )-1- -2sin45°+(3-π)0.20. 先化简,再求值: ÷( -1),其中a=3+ ,b=3- .21. 有A、B两个口袋,A口袋中装有两个分别标有数字2,3的小球;B口袋中装有三个分别标有数字-1,4,-5的小球.小斌先从A口袋中随机取出一个小球,用m表示所取球上的数字,再从B口袋中随机取出两个小球,用n表示所取球上的数字之和.
(1)、用树状图法表示小斌所取出的三个小球的所有可能结果;(2)、求 的值是正数的概率.22. 安装在屋顶的太阳能热水器的横截面示意图如图所示.已知安装集热管的支架AE与支架BF所在直线相交于水箱横截面⊙O的圆心O,支架BF的长度为0.9m,且与屋面AB垂直,支架AE的长度为1.9m,且与铅垂线OD的夹角为35°,支架的支撑点A、B在屋面上的距离为 m.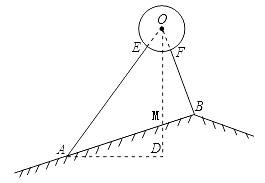 (1)、求⊙O的半径;(2)、求屋面AB与水平线AD的夹角.23. 课外阅读是提高学生素养的重要途径.某校为了解本校学生课外阅读情况,对八年级学生进行随机抽样调查.如图是根据调查结果绘制成的统计图(不完整),请根据图中提供的信息,解答下面的问题:
(1)、求⊙O的半径;(2)、求屋面AB与水平线AD的夹角.23. 课外阅读是提高学生素养的重要途径.某校为了解本校学生课外阅读情况,对八年级学生进行随机抽样调查.如图是根据调查结果绘制成的统计图(不完整),请根据图中提供的信息,解答下面的问题: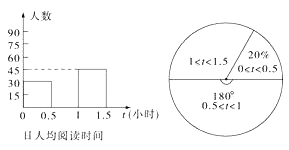 (1)、本次抽样调查的样本容量是;(2)、在条形统计图补中,计算出日人均阅读时间在0.5~1小时的人数是 , 并将条形统计图补充完整;(3)、在扇形统计图中,计算出日人均阅读时间在1~1.5小时对应的圆心角度数度;(4)、根据本次抽样调查,试估计该市15000名八年级学生中日人均阅读时间在0.5~1.5小时的人数.24. 已知:如图,在△ABC中,AB=AC=10,M为底边BC上任意一点,过点M分别作AB、AC的平行线,交AC于点P,交AB于点Q.
(1)、本次抽样调查的样本容量是;(2)、在条形统计图补中,计算出日人均阅读时间在0.5~1小时的人数是 , 并将条形统计图补充完整;(3)、在扇形统计图中,计算出日人均阅读时间在1~1.5小时对应的圆心角度数度;(4)、根据本次抽样调查,试估计该市15000名八年级学生中日人均阅读时间在0.5~1.5小时的人数.24. 已知:如图,在△ABC中,AB=AC=10,M为底边BC上任意一点,过点M分别作AB、AC的平行线,交AC于点P,交AB于点Q.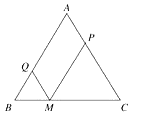 (1)、求四边形AQMP的周长;(2)、M位于BC的什么位置时,四边形AQMP为菱形?说明你的理由.25. “六一”前夕,某玩具经销商用去2350元购进A、B、C三种新型的电动玩具共50套,并且购进的三种玩具都不少于10套,设购进A种电动玩具x套,购进B种电动玩具y套,三种电动玩具的进价和售价如下表:
(1)、求四边形AQMP的周长;(2)、M位于BC的什么位置时,四边形AQMP为菱形?说明你的理由.25. “六一”前夕,某玩具经销商用去2350元购进A、B、C三种新型的电动玩具共50套,并且购进的三种玩具都不少于10套,设购进A种电动玩具x套,购进B种电动玩具y套,三种电动玩具的进价和售价如下表:电动玩具型号
A
B
C
进价(单位:元/套)
40
55
50
销售价(单位:元/套)
50
80
65
(1)、用含x、y的代数式表示购进C种电动玩具的套数;(2)、求出y与x之间的函数关系式;(3)、假设所购进的电动玩具全部售出,且在购销这批玩具过程中需要另外支出各种费用共200元.①求出利润P(元)与x(套)之间的函数关系式;
②求出利润的最大值,并写出此时购进三种电动玩具各多少套?
26. 如图,已知点E在△ABC的边AB上,∠C=90°,∠BAC的平分线交BC于点D,且D在以AE为直径的⊙O上. (1)、求证:BC是⊙O的切线;(2)、若DC=4,AC=6,求圆心O到AD的距离;(3)、若tan∠DAC= ,求 的值.27. 如图,在平面直角坐标系中,抛物线y=ax2+bx+4经过A(-3,0)、B(4,0)两点,且与y轴交于点C,点D在x轴的负半轴上,且BD=BC.动点P从点A出发,沿线段AB以每秒1个单位长度的速度向点B移动,同时动点Q从点C出发,沿线段CA以某一速度向点A移动.
(1)、求证:BC是⊙O的切线;(2)、若DC=4,AC=6,求圆心O到AD的距离;(3)、若tan∠DAC= ,求 的值.27. 如图,在平面直角坐标系中,抛物线y=ax2+bx+4经过A(-3,0)、B(4,0)两点,且与y轴交于点C,点D在x轴的负半轴上,且BD=BC.动点P从点A出发,沿线段AB以每秒1个单位长度的速度向点B移动,同时动点Q从点C出发,沿线段CA以某一速度向点A移动.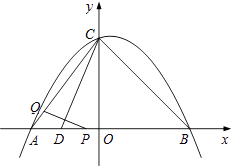 (1)、求该抛物线的解析式;(2)、若经过t秒的移动,线段PQ被CD垂直平分,求此时t的值;(3)、该抛物线的对称轴上是否存在一点M,使MQ+MA的值最小?若存在,求出点M的坐标;若不存在,请说明理由.
(1)、求该抛物线的解析式;(2)、若经过t秒的移动,线段PQ被CD垂直平分,求此时t的值;(3)、该抛物线的对称轴上是否存在一点M,使MQ+MA的值最小?若存在,求出点M的坐标;若不存在,请说明理由.