贵州省遵义市2018届数学中考模拟试卷（2）
试卷更新日期：2018-04-28 类型：中考模拟
一、选择题
-
1. 零上13℃记作＋13℃，零下2℃可记作（ ）
A、2 B、－2 C、－2℃ D、2℃2. 下列汽车标志中既是轴对称又是中心对称图形的是（ ）A、
B、
C、
D、
3. 化简m(m－1)－m2的结果是（ ）
A、m B、－m C、－2m D、2m4. 下列各数中，为不等式组 解的是（ ）
A、－1 B、0 C、2 D、45. 长度单位1纳米＝10－9米，2014年肆虐西非的埃博拉病毒已致大量人员死亡，该病毒直径为直径大约80纳米，用科学记数法表示该病毒直径是（ ）
A、80×10－9米 B、0.8×10－7米 C、8×108米 D、8×10－8米6. 如图，已知AB∥DE，∠ABC＝70°，∠CDE＝140°，则∠BCD的值为（ ）
A、20° B、30° C、40° D、70°7. 一组数据：3，2，1，2，2的众数，中位数，方差分别是（ ）A、2，1，0.4 B、2，2，0.4 C、3，1，2 D、2，1，0.28. 如图，△ABC∽△DEF，相似比为1∶2，若BC＝1，则EF的长是（ ）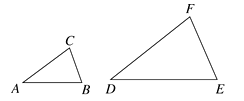
A、1 B、2 C、3 D、49.在一次800米的长跑比赛中，甲、乙两人所跑的路程s（米）与各自所用时间t（秒）之间的函数图象分别为线段OA和折线OBCD，则下列说法正确的是（ ）
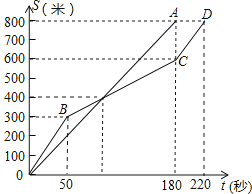A、甲的速度随时间的增加而增大 B、乙的平均速度比甲的平均速度大 C、在起跑后第180秒时，两人相遇 D、在起跑后第50秒时，乙在甲的前面10. 如图，矩形ABCD中，点E在边AB上，将矩形ABCD沿直线DE折叠，点A恰好落在边BC的点F处．若AE＝5，BF＝3，则CD的长是（ ）
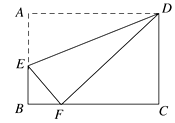A、7 B、8 C、9 D、1011. 如图，⊙O是△ABC的外接圆，已知∠ABO＝40°，则∠ACB的大小为（ ）
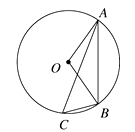A、30° B、40° C、50° D、60°12. 将正整数1、2、3、4、5…，按以下方式排放：
则根据排放规律，从2016到2018的箭头依次为（ ）
A、↓，→ B、→，↑ C、↑，→ D、→，↓二、填空题
-
13. 计算： × ＝.14. 在实数范围内因式分解：x2y－3y＝.
15. 若x、y为实数，且 ＋|y＋1|＝0，则x－y＝.
16. 如图，菱形ABCD的对角线AC、BD相交于点O，且AC＝8，BD＝6，过点O作OH丄AB，垂足为H，则点O到边AB的距离OH＝.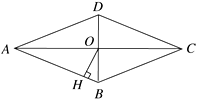
17. 已知m2－5m－1＝0，则2m2－5m＋ ＝
18. 如图，点A(m，2)，B(5，n)在函数y＝ (k＞0，x＞0)的图象上，将该函数图象向上平移2个单位长度得到一条新的曲线，点A、B的对应点分别为A′、B′.图中阴影部分的面积为8，则k的值为.
三、解答题
-
19. 计算： ＋ －( )－1－(2017＋ )0.20. 先化简再求值：( ＋1)÷ ，其中a＝2＋ .21. 如图，△ABC和△ADE都是等腰三角形，且∠BAC＝90°，∠DAE＝90°，B，C，D在同一条直线上．求证：BD＝CE.
22. 在“首届中国西部(银川)房·车生活文化节”期间，某汽车经销商推出A、B、C、D四种型号的小轿车共1000辆进行展销．C型号轿车销售的成交率为50%，其它型号轿车的销售情况绘制在图1和图2两幅尚不完整的统计图中．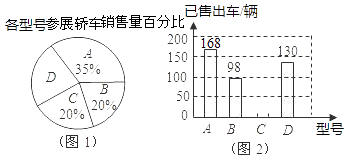
(1)、参加展销的D型号轿车有多少辆？(2)、请你将图2的统计图补充完整；(3)、若对已售出轿车进行抽奖，现将已售出A、B、C、D四种型号轿车的发票(一车一票)放到一起，从中随机抽取一张，求抽到A型号轿车发票的概率．23. 为纪念遵义会议80周年献礼，遵义市政府对城市建设进行了整改，如图，已知斜坡AB长60 米，坡角(即∠BAC)为45°，BC⊥AC，现计划在斜坡中点D处挖去部分斜坡，修建一个平行于水平线CA的休闲平台DE和一条新的斜坡BE(下面两个小题结果都保留根号)．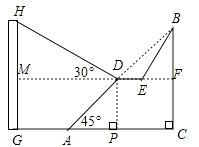
(1)、若修建的斜坡BE的坡比为 ∶1，求休闲平台DE的长是多少米？(2)、一座建筑物GH距离A点33米远(即AG＝33米)，小亮在D点测得建筑物顶部H的仰角(即∠HDM)为30°.点B、C、A、G、H在同一个平面内，点C、A、G在同一条直线上，且HG⊥CG，问建筑物GH高为多少米？24. 已知：△ABC是边长为4的等边三角形，点O在边AB上，⊙O过点B且分别与边AB，BC相交于点D，E，EF⊥AC，垂足为F.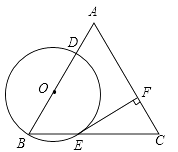
(1)、求证：直线EF是⊙O的切线；(2)、当直线DF与⊙O相切时，求⊙O的半径．25. 某地为了鼓励居民节约用水，决定实行两级收费制，即每月用水量不超过12吨(含12吨)时，每吨按政府补贴优惠价收费；每月超过12吨，超过部分每吨按市场调节价收费，小黄家1月份用水24吨，交水费42元.2月份用水20吨，交水费32元．
(1)、求每吨水的政府补贴优惠价和市场调节价分别是多少元；
(2)、设每月用水量为x吨，应交水费为y元，写出y与x之间的函数关系式；
(3)、小黄家3月份用水26吨，他家应交水费多少元？
26. 如图，在△ABC中，∠C＝90°，AC＝4cm，BC＝5cm，点D在BC上，且CD＝3cm.动点P、Q分别从A、C两点同时出发，其中点P以1cm/s的速度沿AC向终点C移动；点Q以 cm/s的速度沿CB向终点B移动．过点P作PE∥CB交AD于点E，设动点的运动时间为x秒．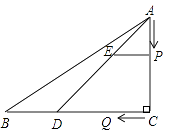
(1)、用含x的代数式表示EP；(2)、当Q在线段CD上运动几秒时，四边形PEDQ是平行四边形；(3)、当Q在线段BD(不包括点B、点D)上运动时，求当x为何值时，四边形EPDQ面积等于 .27. 如图，在平面直角坐标系xOy中，直线y＝x＋3交x轴于A点，交y轴于B点，过A、B两点的抛物线y＝－x2＋bx＋c交x轴于另一点C，点D是抛物线的顶点．
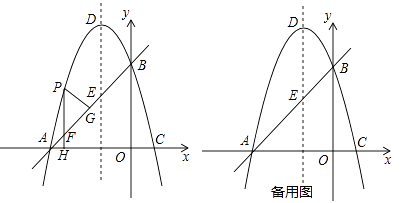(1)、求此抛物线的解析式；(2)、点P是直线AB上方的抛物线上一点(不与点A、B重合)，过点P作x轴的垂线交x轴于点H，交直线AB于点F，作PG⊥AB于点G.求出△PFG的周长最大值；(3)、在抛物线y＝ax2＋bx＋c上是否存在除点D以外的点M，使得△ABM与△ABD的面积相等？若存在，请求出此时点M的坐标；若不存在，请说明理由．