贵州省遵义市2018届数学中考模拟试卷(1)
试卷更新日期:2018-04-28 类型:中考模拟
一、选择题
-
1. 在-4,0,-1,3这四个数中,既不是正数又不是负数的数是( )
A、-4 B、0 C、-1 D、32.由5个完全相同的正方体组成的立体图形如图所示,则它的俯视图是( )
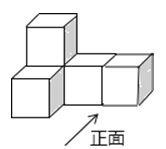 A、
A、 B、
B、 C、
C、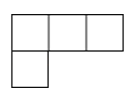 D、
D、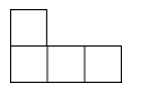 3. 如图,直线AB∥CD,直线EF分别与直线AB,CD相交于点G,H.若∠1=135°,则∠2的度数为( )
3. 如图,直线AB∥CD,直线EF分别与直线AB,CD相交于点G,H.若∠1=135°,则∠2的度数为( )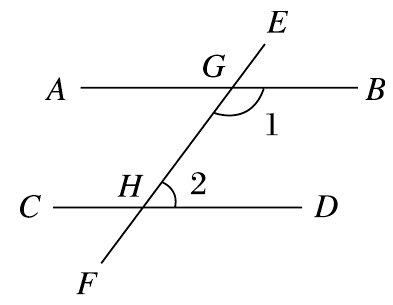 A、35° B、45° C、55° D、65°4. 计算(a2b)3的结果是( )A、a6b3 B、a2b3 C、a5b3 D、a6b5. 2016年我市参加中考的学生的为85000人.将数据85000用科学记数法表示为( )
A、35° B、45° C、55° D、65°4. 计算(a2b)3的结果是( )A、a6b3 B、a2b3 C、a5b3 D、a6b5. 2016年我市参加中考的学生的为85000人.将数据85000用科学记数法表示为( )
A、85×103 B、8.5×103 C、0.85×105 D、8.5×1046. 正六边形的内角和为( )A、1080° B、900° C、720° D、540°7. 不等式2x-4≤0的解集在数轴上表示为( )
A、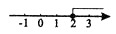 B、
B、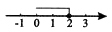 C、
C、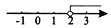 D、
D、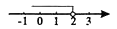 8. 下列调查中,最适合用普查方式的是( )A、调查某中学九年级一班学生视力情况 B、调查一批电视机的使用寿命情况 C、调查遵义市初中学生锻炼所用的时间情况 D、调查遵义市初中学生利用网络媒体自主学习的情况9. 今年“五一”节,小明外出爬山,他从山脚爬到山顶的过程中,中途休息了一段时间,设他从山脚出发后所用的时间为t(分钟),所走的路程为s(米),s与t之间的函数关系如图所示,下列说法错误的是( )
8. 下列调查中,最适合用普查方式的是( )A、调查某中学九年级一班学生视力情况 B、调查一批电视机的使用寿命情况 C、调查遵义市初中学生锻炼所用的时间情况 D、调查遵义市初中学生利用网络媒体自主学习的情况9. 今年“五一”节,小明外出爬山,他从山脚爬到山顶的过程中,中途休息了一段时间,设他从山脚出发后所用的时间为t(分钟),所走的路程为s(米),s与t之间的函数关系如图所示,下列说法错误的是( ) A、小明中途休息用了20分钟 B、小明休息前爬上的速度为每分钟70米 C、小明在上述过程中所走的路程为6600米 D、小明休息前爬山的平均速度大于休息后爬山的平均速度10. 如图,在⊙O中,弦AC∥半径OB,∠BOC=50°,则∠OAB的度数为( )
A、小明中途休息用了20分钟 B、小明休息前爬上的速度为每分钟70米 C、小明在上述过程中所走的路程为6600米 D、小明休息前爬山的平均速度大于休息后爬山的平均速度10. 如图,在⊙O中,弦AC∥半径OB,∠BOC=50°,则∠OAB的度数为( )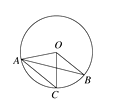 A、25° B、50° C、60° D、30°11. 如图,已知双曲线y= (k<0)经过直角三角形OAB斜边OA的中点D,且与直角边AB相交于点C.若点A的坐标为(-6,4),则△AOC的面积为( )
A、25° B、50° C、60° D、30°11. 如图,已知双曲线y= (k<0)经过直角三角形OAB斜边OA的中点D,且与直角边AB相交于点C.若点A的坐标为(-6,4),则△AOC的面积为( )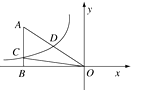 A、4 B、6 C、9 D、1212. 如图,都是由同样大小的圆按一定的规律组成,其中,第①个图形中一共有2个圆;第②个图形中一共有7个圆;第③个图形中一共有16个圆;第④个图形中一共有29个圆;…;则第⑦个图形中圆的个数为( )
A、4 B、6 C、9 D、1212. 如图,都是由同样大小的圆按一定的规律组成,其中,第①个图形中一共有2个圆;第②个图形中一共有7个圆;第③个图形中一共有16个圆;第④个图形中一共有29个圆;…;则第⑦个图形中圆的个数为( ) A、121 B、113 C、105 D、92
A、121 B、113 C、105 D、92二、填空题
-
13. 分解因式:4a2-b2=.14. 某同学遇到一道不会做的选择题,在四个选项中有且只有一个是正确的,则他选对的概率是 .
15. 菱形的两条对角线的长分别是6cm和8cm,则菱形的周长是cm.16. 通信市场竞争日益激烈,某通信公司的手机本地话费标准按原标准每分钟降低a元后,再次下调了20%,现在收费标准是每分钟b元,则原收费标准每分钟是元.
17. 若 +a=3,则( -a)2的值是 .
18. 如图,两条抛物线y1=- x2+1、y2=- x2-1与分别经过点(-2,0),(2,0)且平行于y轴的两条平行线圈成的阴影部分的面积为 .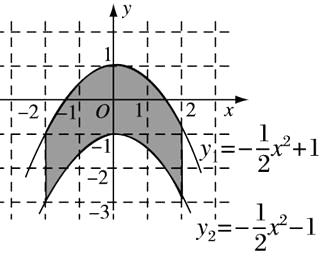
三、解答题
-
19. 计算: -|-4|-2cos45°-(3-π)0.
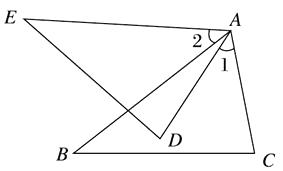
20. 解方程: = -1.21. 已知:如图,AB=AE,∠1=∠2,∠B=∠E.求证:BC=ED.
 22. 某班在一次班会课上,就“遇见老人摔倒后如何处理”的主题进行讨论,并对全班50名学生的处理方式进行统计,得出相关统计表和统计图.
22. 某班在一次班会课上,就“遇见老人摔倒后如何处理”的主题进行讨论,并对全班50名学生的处理方式进行统计,得出相关统计表和统计图.组别
A
B
C
D
处理方式
迅速离开
马上救助
视情况而定
只看热闹
人数
m
30
n
5
请根据表图所提供的信息回答下列问题:
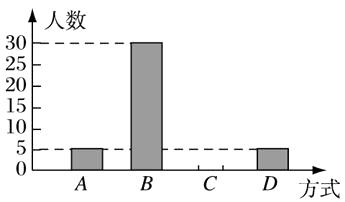 (1)、统计表中的m= , n=;(2)、补全频数分布直方图;
(1)、统计表中的m= , n=;(2)、补全频数分布直方图;
(3)、若该校有2000名学生,请据此估计该校学生采取“马上救助”方式的学生有多少人?23. 数学兴趣小组想利用所学的知识了解某广告牌的高度,已知CD=2m,经测量,得到其它数据如图所示.其中∠CAH=30°,∠DBH=60°,AB=10m.请你根据以上数据计算广告牌的高度GH的长.( ≈1.73,要求结果精确到0.1m) 24. 有5张形状、大小和质地都相同的卡片,正面分别写有字母:A,B,C,D,E和一个等式,背面完全一致.现将5张卡片分成两堆,第一堆:A,B,C;第二堆:D,E,并从第一堆中抽出第一张卡片,再从第二堆中抽出第二张卡片,背面向上洗匀.
24. 有5张形状、大小和质地都相同的卡片,正面分别写有字母:A,B,C,D,E和一个等式,背面完全一致.现将5张卡片分成两堆,第一堆:A,B,C;第二堆:D,E,并从第一堆中抽出第一张卡片,再从第二堆中抽出第二张卡片,背面向上洗匀. (1)、请用画树形图或列表法表示出所有可能结果;(卡片可用A,B,C,D,E表示)(2)、将“第一张卡片上x的值是第二张卡片中方程的解”记作事件M,求事件M的概率.
(1)、请用画树形图或列表法表示出所有可能结果;(卡片可用A,B,C,D,E表示)(2)、将“第一张卡片上x的值是第二张卡片中方程的解”记作事件M,求事件M的概率.
25. 某商场第一次用10000元购进甲、乙两种商品,销售完成后共获利2200元,其中甲种商品每件进价60元,售价70元;乙种商品每件进价50元,售价65元.
(1)、求该商场购进甲、乙两种商品各多少件?
(2)、商场第二次以原进价购进甲、乙两种商品,且购进甲、乙商品的数量分别与第一次相同,甲种商品按原售价出售,而乙种商品降价销售,要使第二次购进的两种商品全部售出后,获利不少于1800元,乙种商品最多可以降价多少元?
26. 如图,已知在△ABP中,C是BP边上一点,∠PAC=∠PBA,⊙O是△ABC的外接圆,AD是⊙O的直径,且交BP于点E.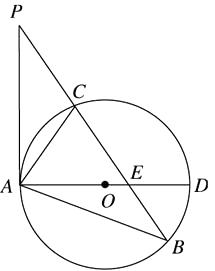 (1)、求证:PA是⊙O的切线;(2)、过点C作CF⊥AD,垂足为点F,延长CF交AB于点G,若AG·AB=12,求AC的长.
(1)、求证:PA是⊙O的切线;(2)、过点C作CF⊥AD,垂足为点F,延长CF交AB于点G,若AG·AB=12,求AC的长.
27. 如图,抛物线y= x2- x-2与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,M是直线BC下方的抛物线上一动点.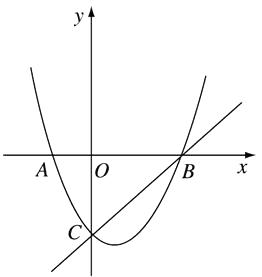 (1)、求A、B、C三点的坐标.(2)、连接MO、MC,并把△MOC沿CO翻折,得到四边形MOM′C,那么是否存在点M,使四边形MOM′C为菱形?若存在,求出此时点M的坐标;若不存在,说明理由.(3)、当点M运动到什么位置时,四边形ABMC的面积最大,并求出此时M点的坐标和四边形ABMC的最大面积.
(1)、求A、B、C三点的坐标.(2)、连接MO、MC,并把△MOC沿CO翻折,得到四边形MOM′C,那么是否存在点M,使四边形MOM′C为菱形?若存在,求出此时点M的坐标;若不存在,说明理由.(3)、当点M运动到什么位置时,四边形ABMC的面积最大,并求出此时M点的坐标和四边形ABMC的最大面积.