山东省济南市历城区2017-2018学年七年级下学期数学期中考试试卷
试卷更新日期:2018-04-28 类型:期中考试
一、选择题
-
1. 骆驼被称为“沙漠之舟”,它的体温是随时间的变化而变化的,在这一问题中,因变量是( )
A、沙漠 B、骆驼 C、时间 D、体温2. 一种新型病毒的直径约为0.000043毫米,用科学记数法表示为( )毫米.A、0.43×10-4 B、0.43×10-5 C、4.3×10-5 D、4.3×10-83. 如图所示,点P到直线l的距离是( )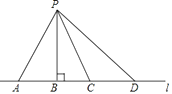 A、线段PA的长度 B、线段PB的长度 C、线段PC的长度 D、线段PD的长度4. 下列计算正确的是( )A、(x3)2=x6 B、x2·x3=x6 C、x+x2=x3 D、x6÷x3=x25.
A、线段PA的长度 B、线段PB的长度 C、线段PC的长度 D、线段PD的长度4. 下列计算正确的是( )A、(x3)2=x6 B、x2·x3=x6 C、x+x2=x3 D、x6÷x3=x25.如图,下列判断正确的是( )
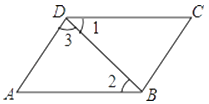 A、若∠1=∠2,则AD∥BC B、若∠1=∠2,则AB∥CD C、若∠A=∠3,则AD∥BC D、若∠A+∠ADC=180°,则AD∥BC6. 用直尺和圆规作一个角等于已知角的示意图如下,则说明∠A′O′B′=∠AOB的依据是( )
A、若∠1=∠2,则AD∥BC B、若∠1=∠2,则AB∥CD C、若∠A=∠3,则AD∥BC D、若∠A+∠ADC=180°,则AD∥BC6. 用直尺和圆规作一个角等于已知角的示意图如下,则说明∠A′O′B′=∠AOB的依据是( ) A、SSS B、SAS C、ASA D、AAS7. 如果(x+1)(5x+a)的乘积中不含x一次项,则a为( )
A、SSS B、SAS C、ASA D、AAS7. 如果(x+1)(5x+a)的乘积中不含x一次项,则a为( )
A、-5 B、5 C、 D、-8. 已知a+b=5,ab=1,则(a-b)2=( )
A、23 B、21 C、19 D、179. 将一副直角三角板如图放置,使含30°角的三角板的一条直角边和45°角的三角板的一条直角边重叠,则∠1的度数为( )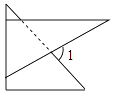 A、45° B、60° C、75° D、85°10. 如图1,在矩形MNPQ中,动点R从点N出发,沿N→P→Q→M方向运动至点M处停止.设点R运动的路程为x,△MNR的面积为y,如果y关于x的函数图象如图2所示,则当x=9时,点R应运动到( )
A、45° B、60° C、75° D、85°10. 如图1,在矩形MNPQ中,动点R从点N出发,沿N→P→Q→M方向运动至点M处停止.设点R运动的路程为x,△MNR的面积为y,如果y关于x的函数图象如图2所示,则当x=9时,点R应运动到( ) A、N处 B、P处 C、Q处 D、M处11. 如图所示, ,若 ,则 ( )
A、N处 B、P处 C、Q处 D、M处11. 如图所示, ,若 ,则 ( ) A、 B、 C、 D、12. 如图,△DAC和△EBC均是等边三角形,A E、BD分别与CD、CE交于点M、N,有如下结论:
A、 B、 C、 D、12. 如图,△DAC和△EBC均是等边三角形,A E、BD分别与CD、CE交于点M、N,有如下结论:①△ACE≌△DCB;②CM=CN;③AC=DN;④∠DAE=∠DBC.其中正确的有( )
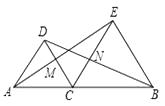 A、②④ B、①②③ C、①②④ D、①②③④
A、②④ B、①②③ C、①②④ D、①②③④二、填空题:
-
13. 一个角的补角是它的余角的4倍,则这个角等于度.14. 一个等腰三角形的底边长为 5,一腰上中线把其周长分成的两部分的差为 3,则这个等腰三角形的腰长为
15. 若 ,则
16. 如图为6个边长相等的正方形的组合图形,则∠1+∠2 +∠3= 度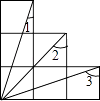 17. 根据如图所示的计算程序计算变量y的对应值,若输入变量x的值为- ,则输出的结果为
17. 根据如图所示的计算程序计算变量y的对应值,若输入变量x的值为- ,则输出的结果为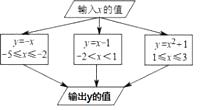 18. 如图, 和 分别是 的内角平分线和外角平分线, 是 的角平分线, 是 的角平分线, 是 的角平分线, 是 的角平分线,若 ,则
18. 如图, 和 分别是 的内角平分线和外角平分线, 是 的角平分线, 是 的角平分线, 是 的角平分线, 是 的角平分线,若 ,则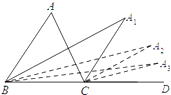
三、解答题:
-
19. 计算:
(1)、
(2)、
(3)、
(4)、 (用乘法公式)
20. 先化简再求值: ﹣ ,其中 .21. 如图,已知∠1+∠3=180°,请说明a∥b.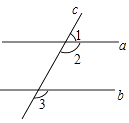 22. 如图,B,C,E,F在同一条直线上,BF=CE,∠B=∠C,AE∥DF,那么AB=CD吗?请说明理由.
22. 如图,B,C,E,F在同一条直线上,BF=CE,∠B=∠C,AE∥DF,那么AB=CD吗?请说明理由. 23. 父亲告诉小明:“距离地面越高,温度越低”,并给小明出示了下面的表格:
23. 父亲告诉小明:“距离地面越高,温度越低”,并给小明出示了下面的表格:距离地面高度(千米)h
0
1
2
3
4
5
温度(℃)t
20
14
8
2
﹣4
﹣10
根据表中,父亲还给小明出了下面几个问题,请你帮助小明回答下列问题:
(1)、表中自变量是;因变量是;当地面上(即h=0时)时,温度是℃.(2)、如果用h表示距离地面的高度,用t表示温度,请写出满足t与h关系的式子.
(3)、计算出距离地面6千米的高空温度是多少?
24. 小凡与小光从学校出发到距学校5千米的图书馆看书,小光直接去图书馆, 小凡途中从路边超市买了一些学习用品,如图反应了他们俩人离开学校的路程s(千米)与时间t(分钟)的关系,请根据图象提供的信息回答问题: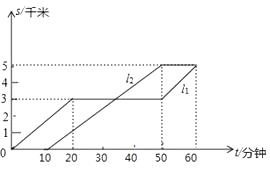 (1)、是描述小凡的运动过程(填 或 );(2)、小凡和小光先出发的是 , 先出发了分钟;
(1)、是描述小凡的运动过程(填 或 );(2)、小凡和小光先出发的是 , 先出发了分钟;
(3)、小凡与小光先到达图书馆的是 , 先到了分钟;
(4)、求小凡与小光从学校到图书馆的平均速度各是多少?(不包括中间停留的时间)25. 如图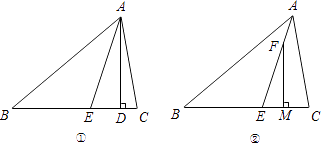 (1)、如图①,在△ABC中,∠B=40°,∠C=80°,AD⊥BC于点D,AE平分∠BAC,求∠EAD的度数;(2)、将(1)中“∠B=40°,∠C=80°”改为“∠B=x°,∠C=y°,∠C>∠B”,
(1)、如图①,在△ABC中,∠B=40°,∠C=80°,AD⊥BC于点D,AE平分∠BAC,求∠EAD的度数;(2)、将(1)中“∠B=40°,∠C=80°”改为“∠B=x°,∠C=y°,∠C>∠B”,①其他条件不变,你能用含x,y的代数式表示∠EAD吗?请写出,并说明理由;
②如图②,AE平分∠BAC,F为AE上一点,FM⊥BC于点M,用含x,y的代数式表示∠EFM,并说明理由.
26. 如图1,点P、Q分别是等边△ABC边AB、BC上的动点(端点除外),点P从顶点A、点Q从顶点B同时出发,且它们的运动速度相同,连接AQ、CP交于点M.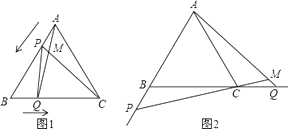 (1)、△ABQ与△CAP全等吗?请说明理由;
(1)、△ABQ与△CAP全等吗?请说明理由;
(2)、当点P、Q分别在AB、BC边上运动时,∠QMC变化吗?若变化,请说明理由;若不变,求出它的度数.(3)、如图2,若点P、Q在运动到终点后继续在AB、BC的延长线上运动,直线AQ、CP交点为M,则∠QMC变化吗?若变化,请说明理由;若不变,则求出它的度数.