山东省青岛市三十九中2017-2018学年八年级下学期数学期中考试试卷
试卷更新日期：2018-04-28 类型：期中考试
一、选择题
-
1. 剪纸是我国最古老民间艺术之一，被列入第四批《人类非物质文化遗产代表作名录》。下列剪纸作品中，是中心对称图形但不是轴对称图形的是（ ）A、
B、
C、
D、
2. 在联欢晚会上，有A，B，C三名同学站在一个三角形的三个顶点位置上，他们在玩抢凳子游戏，要求在他们中间放一个木凳，谁先抢到凳子谁获胜，为使游戏公平，则凳子应放的最适当的位置在△ABC的（ ）
A、三边中线的交点 B、三边中垂线的交点 C、三边上高的交点 D、三条角平分线的交点3. 已知x＞y，则下列不等式不成立的是（ ）
A、-3x+6＞-3y+6 B、2x＞2y C、-3x＜-3y D、x-6＞y-64. 直线 与表示三条相互交叉的公路，现要三条公路的内部建个货物中转站，要求它到三条公路的距离相等，那么选择油库的位置有（ ）处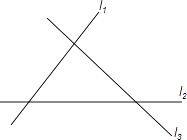
A、1 B、2 C、3 D、45. 关于x的不等式x-b＞0恰有两个负整数解，则b的取值范围是（ ）
A、-3＜b＜-2 B、-3≤b＜-2 C、-3≤b≤-2 D、-3＜b≤-26. 已知一次函数y=kx+b(k，b是常数，且k≠0)，x与y的部分对应值如下表所示，那么不等式kx+b＜0的解集是（ ）x
-2
-1
0
1
2
3
y
3
2
1
0
-1
-2
A、x＜0 B、x＞0 C、x＞1 D、x＜17. 一个等腰三角形底边的长为5cm，一腰上的中线把其周长分成的两部分的差为3cm，则腰长为（ ）
A、2cm B、2cm或8cm C、8cm D、10cm8. 如图，0是正△ABC内一点，OA=3，OB=4，OC=5，将线段B0以点B为旋转中心逆时针旋转60°得到线段BO′，下列结论：①点0与0′的距离为4；②∠AOB=150°；③ = .其中正确的结论是（ ）
A、① B、①② C、②③ D、①②③二、填空题
-
9. 不等式(a-b)x＞a-b的解集是x＜1，则a与b的大小关系是.
10. 命题“如果两个角都是直角，那么这两个角相等”的逆命题.
11. 编队飞行(即平行飞行)的两架飞机A、B在直角坐标系中的坐标分别为A(-1，2)、B(-2，3)，当飞机A飞到指定位置的坐标是(2，-1)时，飞机B的坐标是.
12. 不等式组 的解集为x＜6m+3，则m的取值范围是.
13. 如图，在△ABC中，∠BAC=60°，点D是BC边上一点，连接AD，过点D分别作DE⊥AB于E，DF⊥AC于F.若AD=10，且DE=DF，则DE的长为.
14. 如图，等边△ABC的边长为6，AD是BC边上的中线，M是AD上的动点，E是AC边上一点，若AE=3，EM+CM的最小值为.
15. 如图，在△ABC中，已知AB=AC，DE垂直平分AC，∠A=50°，则∠DCB的度数是.
16. 在直角坐标系中，0为坐标原点，已知点A(1，2)，在y轴的正半轴上确定点P，使△AOP为等腰三角形，则点P的坐标为.
三、作图题:
-
17. 已知：线段a，m.
求作：△ABC，使AB=AC，BC=a，中线AD=m.
四、解答题
-
18. 计算题
(1)、解不等式2x+9≥3(x+2)
(2)、解不等式组 并写出其整数解。
(3)、已知二元一次方程组 的解x、y均是正数，①求a的取值范围；
②化简|4a+5|-|a-4|.
19. 如图，方格纸中每个小正方形的边长都是1个单位长度，Rt△ABC的三个顶点A(-2，2)，B(0，5)，C(0，2).
(1)、将△ABC以点C为旋转中心旋转180°，得到△A1B1C，请画出△A1B1C的图形；
(2)、平移△ABC，使点A的对应点A2坐标为(-2，-6)，请画出平移后对应的△A2B2C2的图形；
(3)、若将△A1B1C绕某一点旋转180°可得到△A1B2C2 ， 请直接写出旋转中心的坐标。
20. 某软件公司开发出一种图书管理软件，前期投入的开发、广告宣传费用共50000元，且每售出一套软件，软件公司还需支付安装调试费用200元。如果每套定价700元，软件公司至少要售出多少套软件才能确保不亏本?
21. 已知：如图，锐角△ABC的两条高BD、CE相交于点O，且OB=OC.求证：△ABC是等腰三角形；
22. 某市的出租车收费y(元)与路程x(千米)之间的函数关系如图所示：
(1)、图中AB段的意义是.(2)、当x＞2时，y与x的函数关系式为.
(3)、张先生打算乘出租车从甲地去丙地，但需途径乙地办点事，已知甲地到乙地的路程为1km，乙地至丙地的路程是3km，现有两种打车方案：方案一：先打车从甲地到乙地，办完事后，再打另一部出租车去丙地
方案二：先打车从甲地到乙地，让出租车司机等候，办完事后，继续乘该车去丙地(出租车等候期间，张先生每分钟另付0.2元，假设计价器不变)
张先生应选择哪种方案较为合算?试说明理由。
23. 某服装公司招工广告承诺：熟练工人每月工资至少3000元。每天工作8小时，一个月工作25天。月工资底薪800元，另加计件工资。加工1件A型服装计酬16元，加工1件B型服装计酬12元。在工作中发现一名熟练工加工1件A型服装和2件B型服装需4小时，加工3件A型服装和1件B型服装需7小时.(工人月工资底薪+计件工资)
(1)、一名熟练工加工1件A型服装和1件B型服装各需要多少小时?
(2)、一段时间后，公司规定：“每名工人每月必须加工A，B两种型号的服装，且加工A型服装数量不少于B型服装的一半”。设一名熟练工人每月加工A型服装a件，工资总额为W元。请你运用所学知识判断该公司在执行规定后是否违背了广告承诺?
24. 如图1，将两个完全相同的三角形纸片ABC和DEC重合放置，其中∠C=90°，∠B=∠E=30°.
(1)、操作发现：如图2，固定△ABC，使△DEC绕点C旋转。当点D恰好落在AB边上时，填空：
①线段DE与AC的位置关系是
②设△BDC的面积为S1 ， △AEC的面积为S2。则S1与S2的数量关系是.
(2)、猜想论证：当△DEC绕点C旋转到图3所示的位置时，小明猜想(1)中S1与S2的数量关系仍然成立，并尝试分别作出了△BDC和△AEC中BC、CE边上的高，请你证明小明的猜想。(3)、拓展探究已知∠ABC=60°，点D是其角平分线上一点，BD=CD=4，DE∥AB交BC于点E(如图4)，若在射线BA上存在点F，使 ，请直接写出相应的BF的长.
-