江苏省高邮市阳光双语初中2018届数学中考一模试卷

试卷更新日期：2018-04-28 类型：中考模拟

进入出卷网下载

一、选择题：

1. 下列图形中，是中心对称图形但不是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 吸烟有害健康．据中央电视台2016年5月30日报道，全世界每年因吸烟引起的疾病致死的人数大约为600万，数据600万用科学记数法表示为（）

A、6×10⁶ B、60×10⁵ C、6×10⁵ D、0.6×10⁷

查看试题解析
3. 下列计算正确的是（）

A、 $2 a^{2} + 2 a^{2} = 2 a^{4}$ B、 $a^{2} \cdot a^{3} = a^{6}$ C、(－2a²)³=－6a⁶ D、a³·a³=a⁶

查看试题解析
4. 如图，将矩形纸带ABCD，沿EF折叠后，C，D两点分别落在C′，D ′的位置，经测量得∠EFB＝65°，则∠AED′的度数是（）

A、65° B、55° C、50° D、25°

查看试题解析
5. 某小组7位学生的中考体育测试成绩（满分60分）依次为57，60，59，57，60，58，60，则这组数据的众数与中位数分别是（）

A、60，59 B、60，57 C、59，60 D、60，58

查看试题解析
6. 一水池有甲、乙、丙三个水管，其中甲、丙两管为进水管，乙管为出水管．单位时间内，甲管水流量最大，丙管水流量最小．先开甲、乙两管，一段时间后，关闭乙管开丙管，又经过一段时间，关闭甲管开乙管．则能正确反映水池蓄水量y（立方米）随时间t（小时）变化的图象是（）

A、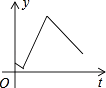 B、 C、 D、

查看试题解析
7.
已知：在Rt△ABC中，∠C=90°，AC=6，BC=8，点E是边AC上一动点，过点E作EF∥BC，交AB边于点F，点D为BC上任一点，连接DE，DF．设EC的长为x，则△DEF的面积y关于x的函数关系大致为（　　）

A、 B、 C、 D、

查看试题解析
8. 已知关于x的一元二次方程（m﹣2）²x²+（2m+1）x+1=0有两个不相等的实数根，则m的取值范围是（）

A、m＞ $\frac{3}{4}$ B、m≥ $\frac{3}{4}$ C、m＞ $\frac{3}{4}$ 且m≠2 D、m≥ $\frac{3}{4}$ 且m≠2

查看试题解析
9. 如图10，是由4个完全相同的小正方体组成的立体图形，则它的俯视图是（）

A、 B、 C、 D、

查看试题解析
10. 哥哥与弟弟的年龄和是18岁，弟弟对哥哥说：“当我的年龄是你现在年龄的时候，你就是18岁”．如果现在弟弟的年龄是x岁，哥哥的年龄是y岁，下列方程组正确的是（）

A、 ${\begin{cases} x = y - 18 \\ y - x = 18 - y \end{cases}$ B、 ${\begin{cases} y - x = 18 \\ x - y = y + 18 \end{cases}$ C、 ${\begin{cases} x + y = 18 \\ y - x = 18 + y \end{cases}$ D、 ${\begin{cases} y = 18 - x \\ 18 - y = y - x \end{cases}$

查看试题解析

二、填空题：

11. 16的算术平方根为.

查看试题解析
12. 一个多边形的每个外角都等于60°，这个多边形的内角和为．

查看试题解析
13. 分解因式：a²b-2ab+b= .

查看试题解析
14. 在一个口袋中有4个完全相同的小球，把它们分别标号为1，2，3，4，随机地摸出一个小球不放回，再随机地摸出一个小球，则两次摸出的小球的标号的和为奇数的概率是.

查看试题解析
15. 如图，在一张正方形纸片上剪下一个半径为r的圆形和一个半径为R的扇形，使之恰好围成图中所示的圆锥，则R与r之间的关系是．

查看试题解析
16. 如图，在平面直角坐标系中，边长为1的正方形OA₁B₁C的对角线A₁C和OB₁交于点M₁；以M₁A₁为对角线作第二个正方形A₂A₁B₂ M₁ ，对角线A₁ M₁和A₂B₂ 交于点M₂；以M₂A₁为对角线作第三个正方形A₃A₁B₃ M₂ ，对角线A₁ M₂和A₃B₃ 交于点M₃；……，依次类推，这样作的第n个正方形对角线交点的坐标为M_n ．

查看试题解析

三、解答题：

17. 计算： $| - 2 | + 2^{- 1} - \cos 60 ° - {(1 - \sqrt{2})}^{0}$

查看试题解析
18. 先化简，再求值：( $\frac{a - 1}{a^{2} - 4 a + 4} - \frac{a + 2}{a^{2} - 2 a}$ )÷( $\frac{4}{a} - 1$ )，其中a＝2－ $\sqrt{3}$ .

查看试题解析
19. 如图，在平行四边形ABCD中，过B作BE⊥CD，垂足为点E，连接AE，F为AE上一点，且∠BFE=∠C．

(1)、求证：△ABF∽△EAD；

(2)、若AB=4，∠BAE=30°，求AE的长；

查看试题解析
20. 某校九年级（2）班的师生步行到距离10千米的山区植树，出发1.5小时后，李明同学骑自行车从学校按原路追赶队伍，结果他们同时到达植树地点．如果李明同学骑车速度是队伍步行速度的2.5倍．求骑车与步行的速度各是多少？

查看试题解析
21. 中学生上学带手机的现象越来越受到社会的关注，为此媒体记者随机调查了某校若干名学生上学带手机的目的，分为四种类型：A接听电话；B收发短信；C查阅资料；D游戏聊天．并将调查结果绘制成图1和图2的统计图（不完整），请根据图中提供的信息，解答下列问题：

(1)、此次抽样调查中，共调查了名学生；

(2)、将图1、图2补充完整；

(3)、现有4名学生，其中A类两名，B类两名，从中任选2名学生，求这两名学生为同一类型的概率（用列表法或树状图法）．

查看试题解析
22. 每个小方格都是边长为1个单位长度的小正方形，△OAB在平面直角坐标系中的位置如图所示．

(1)、将△OAB先向右平移5个单位，再向上平移3个单位，得到△O₁A₁B₁ ，请画出△O₁A₁B₁并直接写出点B₁的坐标；

(2)、将△OAB绕原点O顺时针旋转90°，得到△OA₂B₂ ，请画出△OA₂B₂ ，并求出点A旋转到A₂时线段OA扫过的面积．

查看试题解析
23. 如图，在平面直角坐标系中，一次函数y=ax+b的图象与反比例函数y= $\frac{k}{x}$ 的图象交于一、三象限内的A、B两点，与x轴交于C点，点A的坐标为（2，m），点B的坐标为（n，-2），tan∠BOC= $\frac{1}{2}$ ．

(1)、求该反比例函数和一次函数的解析式．

(2)、求△BOC的面积．

(3)、P是x轴上的点，且△PAC的面积与△BOC的面积相等，求P点的坐标．

查看试题解析
24. 如图，在Rt△ABC中，∠ABC=90°，AC的垂直平分线分别与AC，BC及AB的延长线相较于点D，E，F，且BF=BC，⊙O是△BEF的外接圆，∠EBF的平分线交EF于点G，交⊙O于点H，连接BD，FH．

(1)、求证：△ABC≌△EBF；

(2)、试判断BD与⊙O的位置关系，并说明理由；

(3)、若AB=1，求HG•HB的值．

查看试题解析
25. 某工厂计划生产A、B两种产品共60件，需购买甲、乙两种材料．生产一件A产品需甲种材料4千克，乙种材料1千克；生产一件B产品需甲、乙两种种材料各3千克．经测算，购买甲、乙两种材料各1千克共需资金60元；购买甲种材料2千克和乙种材料3千克共需资金155元．

(1)、甲、乙两种材料每千克分别是多少元？

(2)、现工厂用于购买甲、乙两种材料的资金不超过9900元，且生产B产品不少于38件，问符合生产条件的生产方案有哪几种？

(3)、在（2）的条件下，若生产一件A产品需加工费40元，若生产一件B产品需加工费50元，应选择那种生产方案，使生产这60件产品的成本最低？（成本=材料费+加工费）

查看试题解析
26. 已知：如图①，在平行四边形ABCD中，AB=12，BC=6，AD⊥BD．以AD为斜边在平行四边形AB CD的内部作Rt△AED，∠EAD=30°，∠AED=90°．

(1)、求△AED的周长；

(2)、若△ AED以每秒2个单位长度的速度沿DC向右平行移动，得到△AE₀D₀ ，当A₀D₀与BC重合时停止移动，设运动时间为t秒，△A₀E₀D₀与△BDC重叠的面积为S，请直接写出 S与t之间的函数关系式，并写出t的取值范围；

(3)、如图②，在（2）中，当△AED停止移动后得到△BEC，将△BEC绕点C按顺时针方向旋转α（0°＜α＜180°），在旋转过程中，B的对应点为B₁ ， E的对应点为E₁ ，设直线B₁E₁与直线BE交于点P、与直线CB交于点Q．是否存在这样的α，使△BPQ为等腰三角形？若存在，求出α的度数；若不存在，请说明理由．

查看试题解析