广东省广州市海珠区等五区2017-2018学年高一上学期数学期末联考试卷
试卷更新日期:2018-04-28 类型:期末考试
一、单选题
-
1. 若 , ,且 ,则 ( )
A、 B、 C、 D、2. 下列四组函数中,表示相同函数的一组是( )
A、 B、 C、 D、3. 下列函数中,值域为 的偶函数是( )A、 B、 C、 D、4. 下列函数在其定义域内既是奇函数,又是增函数的是( )A、 B、 C、 D、5. 设 ,则 的大小关系是( )A、 B、 C、 D、6. 函数 的零点所在的一个区间是( )A、 B、 C、 D、7. 设函数 ( )A、3 B、6 C、 D、8. 函数 的图象的大致形状是( )A、 B、
B、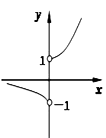 C、
C、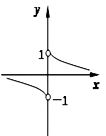 D、
D、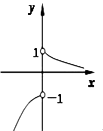 9. 直线 与圆 交点的个数为( )A、2个 B、1个 C、0个 D、不确定10. 圆 与圆 的位置关系是( )A、相离 B、外切 C、相交 D、内切11. 设 是两个不同的平面, 是一条直线,以下命题正确的是( )A、若 ,则 B、若 ,则 C、若 ,则 D、若 ,则12. 某几何体的三视图如下图所示,它的体积为( )
9. 直线 与圆 交点的个数为( )A、2个 B、1个 C、0个 D、不确定10. 圆 与圆 的位置关系是( )A、相离 B、外切 C、相交 D、内切11. 设 是两个不同的平面, 是一条直线,以下命题正确的是( )A、若 ,则 B、若 ,则 C、若 ,则 D、若 ,则12. 某几何体的三视图如下图所示,它的体积为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
13. 计算 .14. 经过 , 两点的直线的倾斜角是 .15. 若函数 在区间[2,3]上的最大值比最小值大 ,则 .16. 体积为8的正方体的顶点都在同一球面上,则该球面的表面积为 .
三、解答题
-
17. 已知 的三个顶点(1)、求 边上高所在直线的方程;(2)、求 的面积 .18. 如图,在直三棱柱 中,已知 , ,设 的中点为D, .

求证:
(1)、 ;(2)、 .19. 已知函数 .(1)、根据定义证明:函数 在 上是增函数;
(2)、根据定义证明:函数 是奇函数.
