四川省广元市2018届高三文数第一次高考适应性统考试卷
试卷更新日期:2018-04-28 类型:高考模拟
一、单选题
-
1. 已知集合 , ,则 ( )A、 B、 C、 D、2. “ 且 ”是“ ”成立的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、即不充分也不必要条件3. 设 是两条不同的直线, 是两个不同的平面,且 ,下列命题中正确的是( )A、若 ,则 B、若 ,则 C、若 ,则 D、若 ,则4. 已知向量 ,且 ,则 的值是( )A、-1 B、 C、- D、5. 若 ,则 ( )A、 B、 C、 D、6. 执行如图所求的程序框图,输出的值是( )
 A、4 B、5 C、6 D、77. 二维空间中,圆的一维测度(周长) ,二维测度(面积) ,三维空间中,球的二维测度(表面积) ,三维测度(体积) ,应用合情推理,若四维空间中,“超球”的三维测度 ,则其四维测度W=( )
A、4 B、5 C、6 D、77. 二维空间中,圆的一维测度(周长) ,二维测度(面积) ,三维空间中,球的二维测度(表面积) ,三维测度(体积) ,应用合情推理,若四维空间中,“超球”的三维测度 ,则其四维测度W=( )
A、 B、 C、 D、8. 已知函数 一个周期内的图象如图所示, , 为图象上的最高点,则 的值为( ) A、 B、 C、 D、9. 在区间[-1,1]上任选两个数 ,则 的概率为( )A、 B、 C、 D、10. 已知定义在 上的函数 的图象关于(1,1)对称, ,若函数 图象与函数 图象的交点为 ,则 ( )A、8072 B、6054 C、4036 D、201811. 函数 ,若关于 的方程 有五个不同的零点,则 的取值范围( )A、(1,2) B、 C、 D、12. 若正项递增等比数列 满足 ,则 的最小值为( )A、 B、 C、 D、
A、 B、 C、 D、9. 在区间[-1,1]上任选两个数 ,则 的概率为( )A、 B、 C、 D、10. 已知定义在 上的函数 的图象关于(1,1)对称, ,若函数 图象与函数 图象的交点为 ,则 ( )A、8072 B、6054 C、4036 D、201811. 函数 ,若关于 的方程 有五个不同的零点,则 的取值范围( )A、(1,2) B、 C、 D、12. 若正项递增等比数列 满足 ,则 的最小值为( )A、 B、 C、 D、二、填空题
-
13. 已知 是实数, 是虚数单位,若 是纯虚数,则 .
14. 设变量 满足约束条件: ,则目标函数 的最小值为 .15. 如图,网格纸上的小正方形边长为1,粗线或虚线表示一个三棱锥的三视图,则此三棱锥的外接球的体积为 .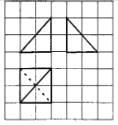 16. 在 中, ,点 是 所在平面内一点,则当 取得最小值时, .
16. 在 中, ,点 是 所在平面内一点,则当 取得最小值时, .三、解答题
-
17. 已知数列 的前 项和 ,且(1)、求数列 的通项公式;(2)、若 ,求数列 的前 项和 .
18. 设函数 .(1)、求 的最大值,并写出使 取最大值时 的集合;(2)、已知 中,角 的对边分别为 ,若 , ,求 的最小值.19. 某中学为研究学生的身体素质与课外体育锻炼时间的关系,对该校200名学生的课外体育锻炼平均每天运动的时间(单位:分钟)进行调查,将收集的数据分成 六组,并作出频率分布直方图(如图),将日均课外体育锻炼时间不低于40分钟的学生评价为“课外体育达标”.附加公式:


 (1)、请根据直方图中的数据填写下面的 列联表,并通过计算判断是否能在犯错误的概率不超过0.01的前提下认为“课外体育达标”与性别有关?
(1)、请根据直方图中的数据填写下面的 列联表,并通过计算判断是否能在犯错误的概率不超过0.01的前提下认为“课外体育达标”与性别有关?
(2)、在[0,10),[40,50)这两组中采取分层抽样,抽取6人,再从这6名学生中随机抽取2人参加体育知识问卷调查,求这2人中一人来自“课外体育达标”和一人来自“课外体育不达标”的概率.
20. 如图四棱锥 ,底面梯形 中, ,平面 平面 ,已知 .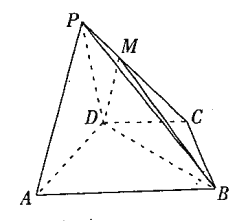 (1)、求证: ;(2)、线段 上是否存在点 ,使三棱锥 体积为三棱锥 体积的6倍.若存在,找出点 的位置;若不存在,说明理由.
(1)、求证: ;(2)、线段 上是否存在点 ,使三棱锥 体积为三棱锥 体积的6倍.若存在,找出点 的位置;若不存在,说明理由.