广东省广州市天河区2017-2018学年七年级上学期数学期末考试试卷

试卷更新日期：2018-04-26 类型：期末考试

进入出卷网下载

一、单选题

1. $| - 2 |$ =（）

A、0 B、-2 C、2 D、1

查看试题解析
2. 下列方程中，解为x=2的方程是（）

A、4x=2 B、3x+6=0 C、 $\frac{1}{2} x = 0$ D、7x-14=0

查看试题解析
3. 下列选项中，两个单项式属于同类项的是（）

A、 $a^{3}$ 与 $b^{3}$ B、 $3 x^{2} y$ 与 $- 4 x^{2} y z$ C、 $x^{2} y$ 与 $- x y^{2}$ D、 $- 2 a^{2} b$ 与 $\frac{1}{2} b a^{2}$

查看试题解析
4. 据统计，到2017年底，广州市的常住人口将达到14330000人，这个人口数据用科学记数法表示为（）

A、 $1433 \times 10^{4}$ B、 $1.433 \times 10^{8}$ C、 $1.433 \times 10^{7}$ D、 $0.1433 \times 10^{8}$

查看试题解析
5. 如图，在直线l上有A，B，C三点，则图中线段共有（）

A、4条 B、3条 C、2条 D、1条

查看试题解析
6. 下列变形中，不正确的是（）

A、 $a - b - (c - d) = a - b - c - d$ B、 $a - (b - c + d) = a - b + c - d$ C、 $a + b - (- c - d) = a + b + c + d$ D、 $a + (b + c - d) = a + b + c - d$

查看试题解析
7. 已知单项式 $- \frac{4 x^{2} y}{3}$ ，下列说法正确的是（）

A、系数是-4，次数是3 B、系数是 $- \frac{4}{3}$ ，次数是3 C、系数是 $\frac{4}{3}$ ，次数是3 D、系数是 $- \frac{4}{3}$ ，次数是2

查看试题解析
8.
如图，它需再添一个面，折叠后才能围成一个正方体，下图中的黑色小正方形分别由四位同学补画，其中正确的是（）

A、 B、 C、 D、

查看试题解析
9. 若 $∠ A$ ， $∠ B$ 互为补角，且 $∠ A < ∠ B$ ，则 $∠ A$ 的余角是（）

A、 $\frac{1}{2} (∠ A + ∠ B)$ B、 $\frac{1}{2} ∠ B$ C、 $\frac{1}{2} (∠ B - ∠ A)$ D、 $\frac{1}{2} ∠ A$

查看试题解析
10. 如图是含 $x$ 的代数式按规律排列的前4行，依此规律，若第10行第2项的值为1034，则此时 $x$ 的值为（）

A、1 B、2 C、5 D、10

查看试题解析

二、填空题

11. 某地1月份的平均气温是零下5℃，用负数表示这个温度是．

查看试题解析
12. 若 $2 a^{x} b^{y} + 4 a^{2} b^{3} = 6 a^{2} b^{3}$ ，则 $y^{x}$ =.

查看试题解析
13. 若代数式 $x - 1$ 和 $3 x + 7$ 的值互为相反数，则 $x =$ .

查看试题解析
14. 已知 $∠ α = 25^{\circ}$ ，那么 $∠ α$ 的补角等于.

查看试题解析
15. 从A处看B处的方向是北偏东21°，反过来，从B看A的方向是.

查看试题解析
16. 如图，把一张长方形纸片沿AB折叠后，若∠1＝50°，则∠2的度数为.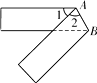

查看试题解析

三、解答题

17. 计算

(1)、计算： $(- 12) - (- 20) + (- 8) - 15$

(2)、计算： $- 2^{2} + 3 \times {(- 1)}^{2016} - 9 \div (- 3)$

查看试题解析
18. 解方程

(1)、解方程： $3 (x + 2) - 1 = x - 3$ ；

(2)、解方程： $\frac{x + 1}{2} - 1 = \frac{2 - x}{3}$

查看试题解析
19. 如图，已知线段AB的长度是xcm，线段BC的长度比线段AB的长度的2倍多1cm，线段AD的长度比线段BC长度的2倍少1cm，求线段BC，AD和CD的长.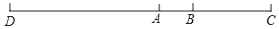

查看试题解析
20. 先化简，再求值： $- x^{2} y + x y^{2} - 3 (x y^{2} - \frac{1}{3} x^{2} y)$ ，其中 $x = \frac{1}{2}$ ， $y = - 1$ .

查看试题解析
21. 根据图中情景信息，解答下列问题：

(1)、购买8根跳绳需元，

(2)、购买11根跳绳需元；

(3)、小红比小明多买2根，付款时小红反而比小明少7元，你认为有这种可能吗？请结合方程知识说明理由.

查看试题解析
22. 解答下面问题：（提示：为简化问题，往往把一个式子看成一个数或一个整体解决问题.）

(1)、若代数式 2 x + 3 y 的值为 − 5 ，求代数式 $4 x + 6 y + 3$ 的值；

(2)、已知 $A = 3 x^{2} - 5 x + 1 ， B = - 2 x + 3 x^{2} - 5$ ，求当 $x = \frac{1}{3}$ 时 $A - B$ 的值.

查看试题解析
23. 如图，已知直线AB和CD相交于点O，在∠COB的内部作射线OE.

(1)、若∠AOC=36°，∠COE=90°，求∠BOE的度数；

(2)、若∠COE：∠EOB：∠BOD=4：3：2，求∠AOE的度数.

查看试题解析
24. 如图的长方形MNPQ是州某市民健身广场的平面示意图，它是由6个正方形拼成的(分别用A，B，C，D，E，F六个字母表示).已知中间最小的正方形A的边长是1米，设正方形C的边长是x米.

(1)、请用含x的代数式分别表示出正方形EF和B的边长；

(2)、观察图形的特点，找出两个等量关系，分别用两种方法列方程求出x的值；

(3)、现沿着长方形广场的四条边铺设下水管道，若甲，乙两个工程队单独铺设分别需要10天和15天完成，如果两队从M处开始，分别沿两个不同方向同时施工 $y$ 天后，因甲队另有任务，余下的工程由乙队单独施工10天完成，求 $y$ 的值.

查看试题解析
25. A，B，C为数轴上三点，若点C到点A的距离是点C到点B的距离的2倍，我们就称点C是【A，B】的和谐点.例如：图1中，点A表示的数为-1，点B表示的数为2。表示1的点C到点A的距离是2，到点B的距离是1.那么点C是【A，B】的和谐点；又如，表示0的点D到点A的距离是1，到点B的距离是2，那么点D就不是【A，B】的和谐点，但点D是【B，A】的和谐点

(1)、若数轴上M，N两点所表示的数分别为 $m ， n$ 且 $m ， n$ 满足 ${(m + 2)}^{2} + | n - 4 | = 0$ ，请求出【M，N】的和谐点表示的数；

(2)、如图2，A，B在数轴上表乐的数分别为-40和20，现有一点P从点B出发向左运动
①若点P到达点A停止，则当P点运动多少个单位时P，A，B中恰有一个点为其余两点的和谐点？
②若点P到达点A后继续向左运动，是否存在使得P，A，B中恰有一个点为其余两点的和谐点的情况？若存在，请直接写出此时PB的距离，若不存在，请说明理由.

查看试题解析