浙江省2018年4月数学学考真题试卷
试卷更新日期:2018-04-25 类型:水平会考
一、选择题
-
1. 已知集合 P={x|0≤x<1},Q={x|2≤x≤3} 记 M=P∪Q ,则( )A、 B、 C、 D、2. 已知函数 的定义域是( )A、 B、 C、 D、R3. 设不等式组 ,所表示的平面区域记为 ,则属于 的点是( )A、 B、 C、 D、4. 已知函数 则 ( )A、1 B、 C、3 D、5. 双曲线 的渐近线是( )
A、 B、 C、 D、6. 如图,在正方体 中,直线 与平面 所成角的余弦值是( )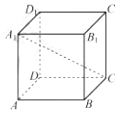 A、 B、 C、 D、7. 若锐角 满足 ,则 ( )A、 B、 C、 D、8. 在三棱锥 中,若 为 的中点,则 ( )A、 B、 C、 D、9. 数列 是公差不为零的等差数列,下列数列中,不构成等差数列的是( )
A、 B、 C、 D、7. 若锐角 满足 ,则 ( )A、 B、 C、 D、8. 在三棱锥 中,若 为 的中点,则 ( )A、 B、 C、 D、9. 数列 是公差不为零的等差数列,下列数列中,不构成等差数列的是( )
A、 B、 C、 D、10. 不等式的 解集是( )A、 B、 C、2 D、11. 用列表法将函数 表示为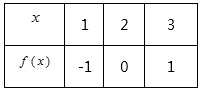 ,则( ) A、 为奇函数 B、 为偶函数 C、 为奇函数 D、 为偶函数12. 如图,在直角坐标系 xOy 中,坐标轴将边长为4的正方形 分割成四个小正方形,若大圆为正方形 xOy 的外接圆,四个小圆圆分别为四个小正方形的内切圆,则图中某个圆的方程是( )
,则( ) A、 为奇函数 B、 为偶函数 C、 为奇函数 D、 为偶函数12. 如图,在直角坐标系 xOy 中,坐标轴将边长为4的正方形 分割成四个小正方形,若大圆为正方形 xOy 的外接圆,四个小圆圆分别为四个小正方形的内切圆,则图中某个圆的方程是( )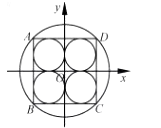 A、 B、 C、 D、13. 设 为实数,则“ ”是 的( )
A、 B、 C、 D、13. 设 为实数,则“ ”是 的( )
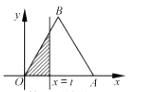
A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件14. 在直角坐标系 xOy 中,已知点 ,过 的直线交 轴于点 ,若直线 的倾斜角是直线 倾斜角的2倍,则 ( )A、 B、 C、 D、15. 甲、乙几何体的三视图分别如图图所示,分别记它们的表面积为 ,体积为 ,则( )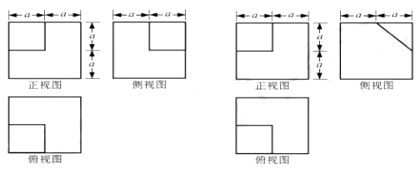 A、 , B、 , C、 , D、 ,16. 如图,设 为椭圆 =1( )的右焦点,过 作 轴的垂线交椭圆于点 ,点 分别为椭圆的右顶点和上顶点, 为坐标原点,若 的面积是 面积的 倍,则该椭圆的离心率( )
A、 , B、 , C、 , D、 ,16. 如图,设 为椭圆 =1( )的右焦点,过 作 轴的垂线交椭圆于点 ,点 分别为椭圆的右顶点和上顶点, 为坐标原点,若 的面积是 面积的 倍,则该椭圆的离心率( )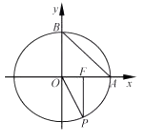 A、 或 B、 或 C、 或 D、 或17. 设a为实数,若函数f(x)=2x2−x+a 有零点,则函数y=f[f(x)]零点的个数是( )
A、 或 B、 或 C、 或 D、 或17. 设a为实数,若函数f(x)=2x2−x+a 有零点,则函数y=f[f(x)]零点的个数是( )
A、1或3 B、2或3 C、2或4 D、3或418. 如图,设矩形 ABCD 所在的平面与梯形 ACEF 所在平面交于 AC ,若 ,则下面二面角的平面角大小为定值的是( )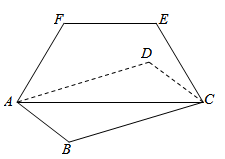 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
19. 已知函数 ,则 的最小正周期是 , 的最大值是.20. 若平面向量 满足 则 .21. 若 中,已知 则 的取值范围是.22. 若不等式 对任意 恒成立,则实数 的最小值是.
三、解答题
-
23. 在等差数列 中, 已知 , ,
(Ⅰ)求 的公差 及通项 ;
(Ⅱ)记 ,求数列的前 项和.