北师大版2017-2018学年数学八年级下学期期中模拟试卷

试卷更新日期：2018-04-24 类型：期中考试

进入出卷网下载

一、单选题

1. 下列条件中，不能判定△ABC是等腰三角形的是（　　）

A、a=3，b=3，c=4 B、a：b：c=2：3：4 C、∠B=50°，∠C=80° D、∠A：∠B：∠C=1：1：2

查看试题解析
2. 下面四个图案中，是轴对称图形但不是旋转对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. △ABC中，∠B=30°，∠C=70°，则∠A的度数是（）

A、70° B、30° C、80° D、90°

查看试题解析
4. 已知实数a、b，若a＞b，则下列结论正确的是（）

A、a﹣5＜b﹣5 B、2+a＜2+b C、 $\frac{a}{3} < \frac{b}{3}$ D、3a＞3b

查看试题解析
5. 如图，已知Rt△ABC中，∠ACB=90°，CD是高，∠A=30°，BD=2cm，求AB的长（　　）

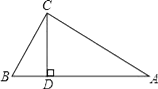A、4 B、6 C、8 D、10

查看试题解析
6. 在一次知识竞赛中，共有16道选择题，评分办法是：答对一题目得6分，答错一题扣2分，不答则不得分也不扣分，得分超过60为合格，明明有两道题未答，问他要达到合格，至少应答对几道题．（　　）

A、9 B、10 C、11 D、12

查看试题解析
7.
如图，Rt△ABC中，∠B=90°，ED是AC的垂直平分线，交AC于点D，交BC于点E．已知∠BAE=10°，则∠C的度数是（）

A、30° B、40° C、50°　　 D、60°

查看试题解析
8. 在平面直角坐标系中，若点P（m，m﹣n）与点Q（﹣2，3）关于原点对称，则点M（m，n）在（）

A、（2，5） B、（﹣3，2） C、（3，﹣2） D、（3，2）

查看试题解析
9. 如图，Rt△ABC中，∠C=90°，AD平分∠BAC，交BC于点D，AB=10，S_△_ABD=15，则CD的长为（）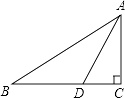

A、3 B、4 C、5 D、6

查看试题解析
10. 一件商品成本价是30元，如果按原价的八五折销售，至少可获得15%的利润．如果设该商品的原价是x元，则列式（）

A、30+30×15%≤85%x B、30+30×15%≥85%x C、30﹣30×15%≤85%x D、30﹣30×15%≥85%x

查看试题解析
11.
如图所示，一次函数y=kx+b（k、b为常数，且k≠0）与正比例函数y=ax（a为常数，且a≠0）相交于点P，则不等式kx+b＞ax的解集是（　　）

A、x＞1 B、x＜1 C、x＞2 D、x＜2

查看试题解析
12. 已知等腰三角形一腰上的高与另一腰的夹角是40°，则这个等腰三角形的底角是（　　）

A、25° B、40° C、65° D、25°或 65°

查看试题解析

二、填空题

13. 如图，△ABC中，∠BAC=100°，EF，MN分别为AB，AC的垂直平分线，则∠FAN= ．

查看试题解析
14. 运行程序如图所示，从“输入实数x”到“结果是否＜18”为一次程序操作，
若输入x后程序操作仅进行了一次就停止，则x的取值范围是．

查看试题解析
15. 如图，已知三角形ABC的面积为12，将三角形ABC沿BC平移到三角形A′B′C′，使B′和C重合，连接AC′交A′C于D，D是A′C的中点，则三角形C′DC的面积为．

查看试题解析
16. 点O是△ABC内一点，且点O到三边的距离相等，∠A=70°，则∠BOC的度数为．

查看试题解析

三、解答题

17. 如图，在Rt△ABC中，∠C=90°，∠A= $\frac{1}{2}$ ∠ABC，BD平分∠ABC，DE⊥AB，CD=4cm，求AB的长．

查看试题解析
18.
如图所示，在△ABC中，AB=CB，∠ABC=90°，F为AB延长线上一点，点E在BC上，且AE=CF．
求证：Rt△ABE≌Rt△CBF．

查看试题解析
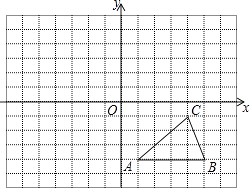
19. 如图所示，方格纸中的每个小方格都是边长为1个单位长度的正方形，建立平面直角坐标系，△ABC的顶点均在格点上．（不写作法）
①以原点O为对称中心，画出△ABC关于原点O对称的△A₁B₁C₁ ，并写出B₁的坐标；
②再把△A₁B₁C₁绕点C₁ ，顺时针旋转90°，得到△A₂B₂C₂ ，请你画出△A₂B₂C₂ ，并写出B₂的坐标．

查看试题解析
20. 当m为何值时
（1）点A（2，3m）关于原点的对称点在第三象限；
（2）点B（3m﹣1，0.5m+2）到x轴的距离等于它到y轴距离的一半？

查看试题解析

四、综合题

21. 解下列不等式（组），并把解集在数轴上表示出来．

(1)、2x﹣1＞ $\frac{3 x - 1}{2}$

(2)、 ${\begin{matrix} x - 2 < 1 \\ \frac{1 - 2 x}{3} \leq 1 \end{matrix}$
．

查看试题解析
22. 为了保护环境，某企业决定购买10台污水处理设备，现有A，B两种型号的设备，其中每台的价格、月处理污水量及年消耗费如表．

A型
B型
价格（万元/台）
12
10
处理污水量（吨/月）
240
200
年消耗费（万元/台）
1
1
预算要求，该企业购买污水处理设备的资金不高于105万元．

(1)、请问该企业有几种购买方案；

(2)、若企业每月产生的污水量为2040吨，为了节约资金，应选择哪种购买方案；

(3)、实际上，该企事业污水的处理方式有两种：A．交污水厂处理厂处理；B．企业购买设备自行处理．如果污水厂处理厂处理污水每吨收费10元，在第（2）问的条件下，该企业自己处理污水与将污水排到污水厂处理相比较，10年节约资金多少万元？

查看试题解析
23. 如图，已知函数y₁=2x+b和y₂=ax﹣3的图象交于点P （﹣2，﹣5），这两个函数的图象与x轴分别交于点A、B．

(1)、分别求出这两个函数的解析式；

(2)、求△ABP的面积；

(3)、根据图象直接写出不等式2x+b＜ax﹣3的解集．

查看试题解析
24. 如图，在△ABC中，∠ABC的平分线与∠ACB的外角的平分线相交于点P，连接AP．

(1)、求证：PA平分∠BAC的外角∠CAM；

(2)、过点C作CE⊥AP，E是垂足，并延长CE交BM于点D．求证：CE=ED．

查看试题解析

	A型	B型
价格（万元/台）	12	10
处理污水量（吨/月）	240	200
年消耗费（万元/台）	1	1