人教版2017-2018学年数学八年级下学期期中模拟试卷
试卷更新日期:2018-04-24 类型:期中考试
一、单选题
-
1. 在下列的线段a、b、c的长为三边的三角形中,不能构成直角三角形的是( )A、a=9,b=41,c=40 B、a=b=5,c=5 C、a:b:c=3:4:5 D、a=11,b=12,c=152. 若平行四边形中两个内角的度数比为1:2,则其中较小的内角是( )A、90° B、60° C、120° D、45°3. 已知一个直角三角形的两条边长分别是6和8,则第三边长是( )A、10 B、8 C、2 D、10或24. 如图,有两棵树,一棵高10米,另一棵高4米,两树相距8米.一只鸟从一棵树的树梢飞到另一棵树的树梢,问小鸟至少飞行( )
 A、8米 B、10米 C、12米 D、14米5. 下列给出的条件中,不能判断四边形ABCD是平行四边形的是( )A、AB∥CD,AD=BC B、∠A=∠C,∠B=∠D C、AB∥CD,AD∥BC D、AB=CD,AD=BC6. 如图,过平行四边形ABCD对角线交点O的直线交AD于E,交BC于F,若AB=5,BC=6,OE=2,那么四边形EFCD周长是( )
A、8米 B、10米 C、12米 D、14米5. 下列给出的条件中,不能判断四边形ABCD是平行四边形的是( )A、AB∥CD,AD=BC B、∠A=∠C,∠B=∠D C、AB∥CD,AD∥BC D、AB=CD,AD=BC6. 如图,过平行四边形ABCD对角线交点O的直线交AD于E,交BC于F,若AB=5,BC=6,OE=2,那么四边形EFCD周长是( )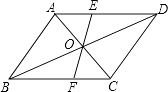 A、16 B、15 C、14 D、137. 如图,直线l过正方形ABCD的顶点B,点A、C至直线l的距离分别为2和3,则此正方形的面积为( )
A、16 B、15 C、14 D、137. 如图,直线l过正方形ABCD的顶点B,点A、C至直线l的距离分别为2和3,则此正方形的面积为( ) A、5 B、6 C、9 D、138. 如图,菱形ABCD中,AB∥y轴,且B(﹣10,1)、C(2,6),则点A的坐标为( )
A、5 B、6 C、9 D、138. 如图,菱形ABCD中,AB∥y轴,且B(﹣10,1)、C(2,6),则点A的坐标为( ) A、(﹣10,12) B、(﹣10,13) C、(﹣10,14) D、(2,12)9. 如图,在矩形纸片ABCD中,已知AD=8,折叠纸片,使AB边与对角线AC重合,点B落在点F处,折痕为AE,且EF=3,则AB的长为( )
A、(﹣10,12) B、(﹣10,13) C、(﹣10,14) D、(2,12)9. 如图,在矩形纸片ABCD中,已知AD=8,折叠纸片,使AB边与对角线AC重合,点B落在点F处,折痕为AE,且EF=3,则AB的长为( ) A、3 B、4 C、5 D、6
A、3 B、4 C、5 D、6二、填空题
-
10. 若实数a,b满足|a+2|+ =0,则a+b= .11. 已知一个直角三角形的两条直角边分别为6cm,8cm,那么这个直角三角形斜边上的高为 cm.12. 计算: = .13. △ABC的周长为16,点D,E,F分别是△ABC的边AB、BC、CA的中点,连接DE,EF,DF,则△DEF的周长是 .14. 一个三角形的三边分别为7cm,24 cm,25 cm,则此三角形的面积为 cm2.15. 如图,今年的冰雪灾害中,一棵大树在离地面3米处折断,树的顶端落在离树杆底部4米处,那么这棵树折断之前的高度是米.
 16. 如图,在矩形ABCD中,对角线AC、BD相交于点O,点E、F分别是AO、AD的中点,若AB=6cm,BC=8cm,则△AEF的周长=cm.
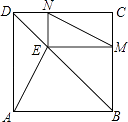
16. 如图,在矩形ABCD中,对角线AC、BD相交于点O,点E、F分别是AO、AD的中点,若AB=6cm,BC=8cm,则△AEF的周长=cm.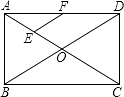 17. 如图,矩形ABCD中,AB=3,BC=4,点E是BC边上一点,连接AE,把∠B沿AE折叠,使点B落在点B′处.当△CEB′为直角三角形时,BE的长为 .
17. 如图,矩形ABCD中,AB=3,BC=4,点E是BC边上一点,连接AE,把∠B沿AE折叠,使点B落在点B′处.当△CEB′为直角三角形时,BE的长为 .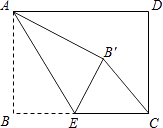
三、解答题
-
18. 已知:如图,在▱ABCD中,对角线AC、BD相交于点O,EF过点O分别交AD、BC于点E、F.求证:OE=OF.
 19. 如图,已知四边形ABCD是菱形,点M、N分别在AB、AD上,且BM=DN,MG∥AD,NF∥AB,点F、G分别在BC、CD上,MG与NF相交于点E,求证:四边形AMEN是菱形.
19. 如图,已知四边形ABCD是菱形,点M、N分别在AB、AD上,且BM=DN,MG∥AD,NF∥AB,点F、G分别在BC、CD上,MG与NF相交于点E,求证:四边形AMEN是菱形. 20. 如图,正方形ABCD中,点E、F分别在AD、CD上,且AE=DF,连接BE、AF,相交于G.求证:AF⊥BE.
20. 如图,正方形ABCD中,点E、F分别在AD、CD上,且AE=DF,连接BE、AF,相交于G.求证:AF⊥BE.
四、计算题
-
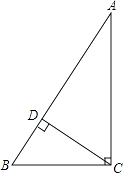
21. 已知,在△ABC中,∠ACB=90°,CD⊥AB垂足为D,BC=6,AC=8,求AB与CD的长.
五、综合题
-
22. 阅读下面材料,回答问题:(1)、在化简 的过程中,小张和小李的化简结果不同;
小张的化简如下: = = = ﹣
小李的化简如下: = = = ﹣
请判断谁的化简结果是正确的,谁的化简结果是错误的,并说明理由.
(2)、请你利用上面所学的方法化简 .
-