浙江省宁波市鄞州区九校2018届九年级下学期数学4月阶段测试试卷
试卷更新日期:2018-04-24 类型:月考试卷
一、选择题
-
1. 在实数 , , , 中,最大的是( )A、 B、 C、 D、2. 下列计算正确的是( )A、(﹣2xy)2=﹣4x2y2 B、x6÷x3=x2 C、(x﹣y)2=x2﹣y2 D、2x+3x=5x3. 左下图是由4个大小相同的正方体组合而成的几何体,其左视图是( )
 A、
A、 B、
B、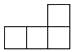 C、
C、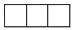 D、
D、 4. 年 月 日国产大型客机 首飞成功圆了中国人的“大飞机梦”,它颜值高性能好,全长近 米,最大载客人数 人,最大航程约 公里,数字 用科学记数法表示为( )A、 B、 C、 D、5. 如图,直线 ,直线 与 , 分别相交于 , 两点, 交 于点 , ,则 的度数是( ).
4. 年 月 日国产大型客机 首飞成功圆了中国人的“大飞机梦”,它颜值高性能好,全长近 米,最大载客人数 人,最大航程约 公里,数字 用科学记数法表示为( )A、 B、 C、 D、5. 如图,直线 ,直线 与 , 分别相交于 , 两点, 交 于点 , ,则 的度数是( ). A、 B、 C、 D、6. 关于 的方程 的一个根为 ,则另一个根为( ).A、 B、 C、 D、7. 某篮球队10名队员的年龄如下表所示:则这10名队员年龄的众数和中位数分别是( )
A、 B、 C、 D、6. 关于 的方程 的一个根为 ,则另一个根为( ).A、 B、 C、 D、7. 某篮球队10名队员的年龄如下表所示:则这10名队员年龄的众数和中位数分别是( )年龄(岁)
18
19
20
21
人数
2
4
3
1
A、19,19 B、19,19.5 C、20,19 D、20,19.58. 如图,五一旅游黄金周期间,某景区规定 和 为入口, , , 为出口,小红随机选一个入口景区,游玩后任选一个出口离开,则她选择从 口进入,从 , 口离开的概率是( ). A、 B、 C、 D、9. 如图,△ABC内接于⊙O,∠A=60°,BC=6 ,则 的长为( )
A、 B、 C、 D、9. 如图,△ABC内接于⊙O,∠A=60°,BC=6 ,则 的长为( ) A、2π B、4π C、8π D、12π10. 如图,正方形 的对角线 , 相交于点 , , 为 上一点, ,连接 ,过点 作 于点 ,与 交于点 ,则 的长为( ).
A、2π B、4π C、8π D、12π10. 如图,正方形 的对角线 , 相交于点 , , 为 上一点, ,连接 ,过点 作 于点 ,与 交于点 ,则 的长为( ).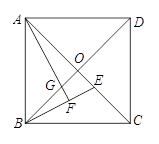 A、 B、 C、 D、11. 如图,为了测量山坡护坡石坝的坡度(坡面的铅直高度与水平宽度的比称为坡度),把一根长 的竹竿 斜靠在石坝旁,量出杆长 处的 点离地面的高度 ,又量的杆底与坝脚的距离 ,则石坝的坡度为( ).
A、 B、 C、 D、11. 如图,为了测量山坡护坡石坝的坡度(坡面的铅直高度与水平宽度的比称为坡度),把一根长 的竹竿 斜靠在石坝旁,量出杆长 处的 点离地面的高度 ,又量的杆底与坝脚的距离 ,则石坝的坡度为( ).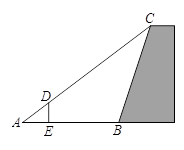 A、 B、 C、 D、12. 在矩形纸片ABCD中,AD=8,AB=6,E是边BC上的点,将纸片沿AE折叠,使点B落在点F处,连接FC,当△EFC为直角三角形时,BE的长为( )
A、 B、 C、 D、12. 在矩形纸片ABCD中,AD=8,AB=6,E是边BC上的点,将纸片沿AE折叠,使点B落在点F处,连接FC,当△EFC为直角三角形时,BE的长为( )
A、3 B、5 C、3或5 D、3或6二、填空题
-
13. 分解因式:14. 圆锥的底面半径为2,母线长为6,则圆锥的侧面积为15. 如图,将△AOB绕点O按逆时针方向旋转45°后得到△COD,若∠AOB=15°,则∠AOD=度
 16. 如图,在平面直角坐标系中,菱形ABOC的顶点O在坐标原点,边BO在x轴的负半轴上,∠BOC=60°,顶点C的坐标为(m, ),反比例函数 的图像与菱形对角线AO交于D点,连接BD,当BD⊥x轴时,k的值是
16. 如图,在平面直角坐标系中,菱形ABOC的顶点O在坐标原点,边BO在x轴的负半轴上,∠BOC=60°,顶点C的坐标为(m, ),反比例函数 的图像与菱形对角线AO交于D点,连接BD,当BD⊥x轴时,k的值是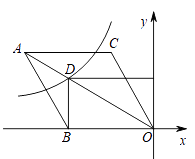
17. 如图,在△ABC中,AC=BC,∠ACB=90°,点D在BC上,BD=3,DC=1,点P是AB上的动点,则PC+PD的最小值为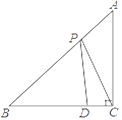 18. 如图,AC是矩形ABCD的对角线,AB=2,BC= ,点E,F分别是线段AB,AD上的点,连接CE,CF,当∠BCE=∠ACF,且CE=CF时,AE+AF=.
18. 如图,AC是矩形ABCD的对角线,AB=2,BC= ,点E,F分别是线段AB,AD上的点,连接CE,CF,当∠BCE=∠ACF,且CE=CF时,AE+AF=.
三、解答题
-
19. 先化简,再求值:(m+2﹣ )• 其中m=﹣ .20. 如图,从热气球C处测得地面A,B两点的俯角分别为 , ,此时热气球C处所在位置到地面上点A的距离为400米.求地面上A,B两点间的距离.
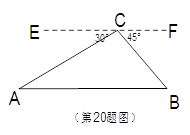 21. 张师傅驾车从甲地去乙地,途中在加油站加了一次油,加油时,车载电脑显示还能行驶 千米.假设加油前、后汽车都以 千米/小时的速度匀速行驶,已知油箱中剩余油量 (升)与行驶时间 (小时)之间的关系如图所示.
21. 张师傅驾车从甲地去乙地,途中在加油站加了一次油,加油时,车载电脑显示还能行驶 千米.假设加油前、后汽车都以 千米/小时的速度匀速行驶,已知油箱中剩余油量 (升)与行驶时间 (小时)之间的关系如图所示.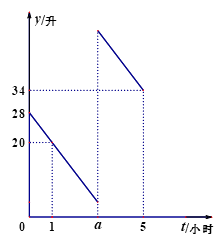 (1)、求张师傅加油前油箱剩余油量 (升)与行驶时间 (小时)之间的关系式;(2)、求出 的值;(3)、求张师傅途中加油多少升?22. 中央电视台的《朗读者》节目激发了同学们的读书热情,为了引导学生“多读书,读好书”,某校对八年级部分学生的课外阅读量进行了随机调查,整理调查结果发现,学生课外阅读的本数最少的有 本,最多的有 本,并根据调查结果绘制了不完整的图表,如下所示:
(1)、求张师傅加油前油箱剩余油量 (升)与行驶时间 (小时)之间的关系式;(2)、求出 的值;(3)、求张师傅途中加油多少升?22. 中央电视台的《朗读者》节目激发了同学们的读书热情,为了引导学生“多读书,读好书”,某校对八年级部分学生的课外阅读量进行了随机调查,整理调查结果发现,学生课外阅读的本数最少的有 本,最多的有 本,并根据调查结果绘制了不完整的图表,如下所示:本数(本)
频数(人数)
频率
合计
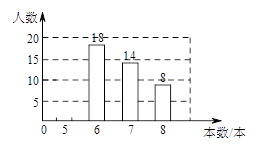 (1)、统计图表中的 a = , b = , c = .(2)、请将频数分布直方图补充完整.(3)、求所有被调查学生课外阅读的平均本数.(4)、若该校八年级共有 1200 名学生,请你估计该校八年级学生课外阅读 7 本及以上的人数.23. 攀枝花芒果由于品质高、口感好而闻名全国,通过优质快捷的网络销售渠道,小明的妈妈先购买了2箱A品种芒果和3箱B品种芒果,共花费450元;后又购买了1箱A品种芒果和2箱B品种芒果,共花费275元(每次两种芒果的售价都不变).(1)、问A品种芒果和B品种芒果的售价分别是每箱多少元?(2)、现要购买两种芒果共18箱,要求B品种芒果的数量不少于A品种芒果数量的2倍,但不超过A品种芒果数量的4倍,请你设计购买方案,并写出所需费用最低的购买方案.24. 如图,△ABC中,以BC为直径的⊙O交AB于点D,AE平分∠BAC交BC于点E,交CD于点F.且CE=CF.
(1)、统计图表中的 a = , b = , c = .(2)、请将频数分布直方图补充完整.(3)、求所有被调查学生课外阅读的平均本数.(4)、若该校八年级共有 1200 名学生,请你估计该校八年级学生课外阅读 7 本及以上的人数.23. 攀枝花芒果由于品质高、口感好而闻名全国,通过优质快捷的网络销售渠道,小明的妈妈先购买了2箱A品种芒果和3箱B品种芒果,共花费450元;后又购买了1箱A品种芒果和2箱B品种芒果,共花费275元(每次两种芒果的售价都不变).(1)、问A品种芒果和B品种芒果的售价分别是每箱多少元?(2)、现要购买两种芒果共18箱,要求B品种芒果的数量不少于A品种芒果数量的2倍,但不超过A品种芒果数量的4倍,请你设计购买方案,并写出所需费用最低的购买方案.24. 如图,△ABC中,以BC为直径的⊙O交AB于点D,AE平分∠BAC交BC于点E,交CD于点F.且CE=CF. (1)、求证:直线CA是⊙O的切线;(2)、若BD= DC,求 的值.25. 定义:有一个内角为 ,且对角线相等的四边形称为准矩形.
(1)、求证:直线CA是⊙O的切线;(2)、若BD= DC,求 的值.25. 定义:有一个内角为 ,且对角线相等的四边形称为准矩形. (1)、① 如图1,准矩形 中, ,若 , ,则 ;
(1)、① 如图1,准矩形 中, ,若 , ,则 ;②如图2,直角坐标系中, , ,若整点 使得四边形 是准矩形,则点 的坐标是;(整点指横坐标、纵坐标都为整数的点)
(2)、如图3,正方形 中,点 、 分别是边 、 上的点,且 ,求证:四边形 是准矩形;(3)、已知,准矩形 中, , , ,当△ 为等腰三角形时,请直接写出这个准矩形的面积是 .26. 如图,抛物线y=x2+bx+c与x轴交于A、B两点,B点坐标为(3,0),与y轴交于点C(0,3). (1)、求抛物线y=x2+bx+c的表达式;(2)、点D为抛物线对称轴上一点,当△BCD是以BC为直角边的直角三角形时,求点D的坐标;(3)、点P在x轴下方的抛物线上,过点P的直线y=x+m与直线BC交于点E,与y轴交于点F,求PE+EF的最大值.
(1)、求抛物线y=x2+bx+c的表达式;(2)、点D为抛物线对称轴上一点,当△BCD是以BC为直角边的直角三角形时,求点D的坐标;(3)、点P在x轴下方的抛物线上,过点P的直线y=x+m与直线BC交于点E,与y轴交于点F,求PE+EF的最大值.